How can I understand the concept of a noise in machine learning?

Question

In Bishop's book, one of the first examples is shown here

Essentially, the data $x$ are randomly generated, and $t$ are generated by running $x$ through a function $\sin(2\pi x)$, then Gaussian noise is added.

I have trouble understanding how this theoretical toy example Gaussian noise translates into real world application.

For example, I am given a data set containing a bunch feature vectors representing spam emails, and a target $\{-1, +1\}$ corresponding to whether or not the user has indicated it is a spam $(+1)$ or not $(-1)$.

I have difficulty seeing where the Gaussian noise in the above example translates into this practical scenario.

Is the noise added when the person who is creating the data set separates the emails into a spam or non-spam (and how)?

I don't quite understanding since, I can imagine going through my mailbox right now and separating spam versus non-spam, and I could do so with 100% accuracy - no noise.

Just knowing that there is some "noise" isn't very helpful (there is pretty much noise in everything in our physical realm), there any actual method of modeling this noise, mathematically speaking?

Answer 1

You can't really have Gaussian noise in your case directly. In Bishop's example, t can take any value between -1 and 1 whereas in your case the only possible values are -1 and 1. If you were modelling a score of how spam the e-mail looks then yes, you could have Gaussian noise.

I will give an example to illustrate the concept of noise in the case you mentioned:

Imagine that you want to set-up a score of how spam an e-mail is, so that you don't need to look at every single e-mail you receive. After you go through 1000 e-mail in your inbox, you think that there are some patterns and you decide to set up some "rules":

• The score starts at 0.
• If there are more than 4 "!" then 0.6 is added to the score
• If the body of the e-mail includes any of the words "offer", "voucher", "deal" then 0.1 is added to the score for each case.
• If the e-mail says "Hi man" then 0.1 is subtracted from it.

and then you specify that if the spam score is 0.7 or above then the e-mail goes in the spam folder.

You can see that there will always be some spam e-mails not captured by the rules and there might be some normal e-mails marked as spam incorrectly. You basically sacrifice some of your 100% accuracy for the convenience of a clean inbox.

For example, you receive an e-mail that says

"Hi man,

I got a great offer for my car!!!! If I manage to sell it, we go to Vegas. Deal?"

In that example, this e-mail would be marked as spam incorrectly and the last word "Deal?" can be considered as the extra "noise" that made your spam classifier go wrong.

Answer 2

"Noise" does not mean that something is wrong, or incorrect, and it does not have to be Gaussian. When we talk about using a statistical model to describe some phenomenon, we have in mind some function $f$ of the features, that is used to predict target variable $y$, i.e. something like

$$ y = f(x) + \varepsilon $$

where $\varepsilon$ is some "noise" (it does not have to be additive). By noise in here, we simply mean the things that is not accurately predicted by our function

$$ y - f(x) = \varepsilon $$

So if $f(x)$ is a very good approximation of $y$, then the "noise" is small (it can be zero if you have perfect fit $y = f(x)$), if it is a bad approximation, it is relatively larger.

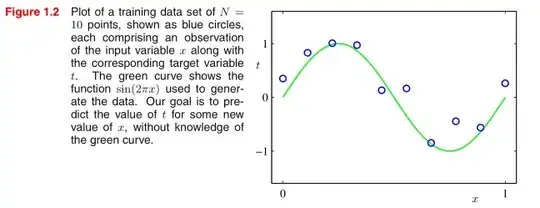
So looking at your picture, the green line is what we predicted, while the blue points is the actual data, noise is the discrepancy between them.

Is the noise added when the person who is creating the data set separates the emails into a spam or non-spam (and how)?

It can be, but it can be also a number of other cases. It can be precision of the measurement device that you used, human errors, but also the data can be noisy, for example, there can be spam e-mails that are almost impossible to distinguish from the valid e-mails, of users can mark valid e-mails as spam ("I don't like this newsletter any more, don't show it to me"), you can also have non-spam e-mails that look very much like spam etc. All this may lead to misclassifications, "noise" is the catch-all term for all such factors.

Just knowing that there is some "noise" isn't very helpful (there is pretty much noise in everything in our physical realm), there any actual method of modeling this noise, mathematically speaking?

Yes, often we build our models in such way, that they also tell us something about what can we expect from the noise. For example, simple linear regression is defined as

$$\begin{align} y &= \beta_0 + \beta_1 x + \varepsilon \\ \varepsilon &~ \sim \mathcal{N}(0, \sigma^2) \end{align}$$

so we assume constant variance, and under this assumption, we estimate the variance of the noise $\sigma^2$, so we can estimate prediction intervals. What you can see from this example, $\varepsilon$ is a random variable. It is random not because someone throws a coin and based on the result, distorts your data, but because it is unpredictable for us (e.g. coin toss is a deterministic process, but we consider it as random). If we would be able to predict when and how exactly our model would be wrong, then we wouldn't be making incorrect predictions in the first place. So the "noise" has some distribution (e.g. Gaussian) that tells us what could be the possible spread of the errors we make when using our model to make predictions. Estimating the distribution is modelling the noise.

Answer 3

In Bishop's example t seems to be the target while x is a determinstic signal. Noise is part of the relationship between the signal and the target. In your spam example that would correspond to the user's labelling being the dependent variable, while some other signals (e.g. the content or sender email address) would be used to predict the user labelling. Noise in this context doesn't mean that the target is not correctly observed, but that the signal itself is noisy, e.g. there is no 1:1 relationship of email address to spam.