Does BoxCox transformation work for logistic regression?

Question

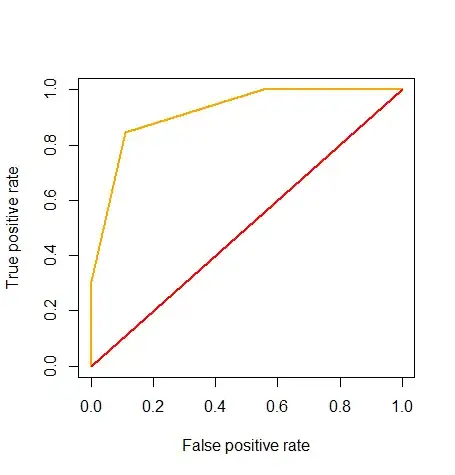
I'm working on a case study from this MIT course. I'm practicing classification problems.

Here is the code for my model. (The dataset can be accessed from the link. I can add it to this post)

    idx <- sample(seq(1, 3), size = nrow(Book), replace = TRUE, 
                  prob = c(.45, .35, .2))
    train <- Book[idx == 1,]
    val <- Book[idx == 2,]
    test <- Book[idx == 3,]
    
    glm.fit1 <- glm(Florence ~., family = binomial, 
                    data = train)
    summary(glm.fit1)
    glm.probs1 <- predict(glm.fit1, test, type='response')
    glm.pred1 <- rep("0",nrow(test))
    glm.pred1[glm.probs1 >.5] <- "1"

This is the confusion matrix

    > table(glm.pred1, test$Florence)
             
    glm.pred1   0   1
            0 787  73
            1   0   1

I have tried a few subsets of predictors and they have performed poorly.

I checked for linearity relationship between the logit of the outcome and each predictor variables.

    # Select only numeric predictors
    num.train <-  num_vars(train)
    # Bind the logit and tidying the data for plot
    num.train <- num.train %>%
      mutate(logit = log(probabilities/(1-probabilities))) %>%
      gather(key = "predictors", value = "predictor.value", 
             -logit)
    
    ggplot(num.train, aes(logit, predictor.value)) + 
      geom_point(size = 0.5, alpha = 0.5) +
      geom_smooth(method = "loess") + 
      theme_bw() + 
      facet_wrap(~predictors, scales = "free_y")

The correlation between my predictors and response are largely weak and the relationships appear to be mostly non-linear. How do you adjust them to fit the assumptions for logistic regression?

1. Monotonic transformations cannot make *non*-monotonic relationships linear. 2. Your response is 0-1, so the logits should all be -infinity or plus infinity. If you're looking at logits of some *fitted* model, that's useless if the model is badly wrong. 3. Your plots seems to be flipped around; you're not trying to predict x's from the response but the other way around; how are these curves useful? — Glen_b, Jan 21 '19 at 02:24
How do you suggest checking for linearity between predictors and a response? — Sebastian, Jan 21 '19 at 02:32
I misspoke. I meant to say - how do you suggest checking for linearity between the logit of the outcome and each predictor? My understanding is that is what gets assumed in logistic regression — Sebastian, Jan 21 '19 at 02:38
The logit of the outcome is not observed (or rather, it is, but they're all $\pm\infty$), and you can't rely on a fitted model's correctness while you're constructing a diagnostic check for its correctness. If you want to ask how to perform diagnostic checks on a logistic regression, again that's a whole new question. — Glen_b, Jan 21 '19 at 02:41
Update: https://stats.stackexchange.com/questions/388305/how-do-i-check-my-logistic-regression-for-linearity — Sebastian, Jan 21 '19 at 03:02
1) the confusion matrix might be informative, but is is based on *accuracy* which is not a proper score function. You should use a proper score function. 2) Model the continuous predictors with splines. — kjetil b halvorsen, Jan 21 '19 at 12:43
At https://stats.stackexchange.com/a/14501/919 I supplied a practical answer to this question. — whuber, Jun 28 '21 at 11:29

score 2 · Answer 1 · answered Dec 02 '21 at 19:38

The box-Cox transformation is used for the dependent (response) variable in regression, and with logistic regression the response is binary, and transforming a binary variable do not make much sense.

If you think about something like Box-Cox for transforming predictors, that is known as Box-Tidwell transformation, but I guess that today using splines is a better idea. Or maybe you just want some way to investigate the linearity of the relationship in logistic regression. That have been asked many times on site, below some relevant earlier posts. See also the comments thread to this post.

Does BoxCox transformation work for logistic regression?

1 Answers1

Linked