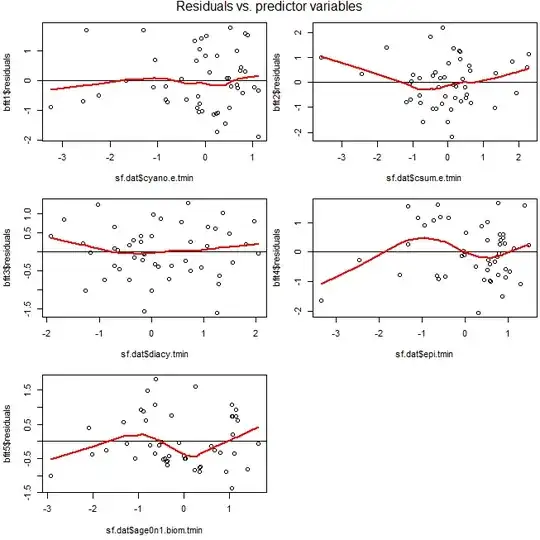
This is a follow-on question from here. I received two conflicting answers to the question posed in the title of this post. The diagnostics of the multiple regression looked okay (see link), but it was recommended there that I use individual residuals vs. predictor variables plots in order to assess the linearity of the component variables that make up the multiple regression. Here they are.
I believe that the two plots on the right and the bottom one are sufficiently non-linear that those data should be further transformed to increase linearity before using them. But do I have still have to do that, given that the multiple regression diagnostics were okay? I haven't found the answer in textbooks.