3

X,Y,Z are non negative random variables which are independent and uniformly distributed in [0,1] and let $\alpha$ be a given number in [0.1]. Now how to compute $\text{Pr}(X+Y+Z>\alpha \;\;\; \& \;\;\; X+Y\leq \alpha)?$

Answer:- Now how to use here step function,laplace transform, inverse laplace transform and convolution integral?

Community
  • 1
Dhamnekar Winod
  • 806
  • 8
  • 17
  • (a) find joint distribution of $(X+Y,X+Y+Z)$ (b) compute $\text{Pr}(X+Y\le\alpha)$ and $\text{Pr}(X+Y+Z>\alpha|X+Y\le\alpha)$ – Xi'an Jan 18 '19 at 13:42
  • I think X,Y,Z should be independent for further analysis. – gunes Jan 18 '19 at 13:48
  • 1
    Please explain how these variables are "dependent" and how that dependency is mathematically represented or known by you. – whuber Jan 18 '19 at 15:08
  • @whuber, You will get answer to this thread here $\Rightarrow$ https://mathhelpboards.com/advanced-probability-statistics-19/joint-cumulative-distribution-dependent-variables-7156.html – Dhamnekar Winod Jan 18 '19 at 15:16
  • @Dhamnekar, in the question statement, X,Y,Z are stated as *dependent*, and in the link you provided, just above your post, it is suspected that the three is actually independent. All solutions in that forum assumes this independence, (as well as Xi'an's comment). – gunes Jan 18 '19 at 18:46
  • @gunes, In the link provided by me, thread author stated X,Y,Z are dependent. That's why I also stated them as dependent. By the way, In that link, in #4 inverse laplace transform have been multiplied by $\frac16$ instead of $\frac12$. Would you tell me why? – Dhamnekar Winod Jan 19 '19 at 07:08
  • 2
    @Dhamnekar, the author also has typo, but the answer just above your post states the independence. Anyway, people here are trying to say that, saying just $X,Y,Z$ are dependent is not enough. Either it must be independent to solve it just as in the link, or you have to give more information about their dependence. For example, is it $X=Y=Z$, or $X=Y^2=Z^3$ or $X=\sqrt{Y}=Z/5$. These are also dependent RVs. Do you think your posted solution covers all of these cases, and return the same answer? – gunes Jan 19 '19 at 07:09
  • 1
    @gunes, I have edited my question stating X, Y,Z are independent. But do you know the answer to my another query about #4 in the link? – Dhamnekar Winod Jan 19 '19 at 07:18

1 Answers1

4

Integrate the density over the region. The density of each variable is the indicator of the interval $[0,1]$, $\mathcal{I}_{[0,1]},$ and the independence assumption implies the multivariate density is the product of these indicators, whence

$$\Pr(X+Y\le\alpha \lt X+Y+Z) = \iiint_{x+y\le\alpha\le x+y+z} \mathcal{I}_{[0,1]}(x)\mathcal{I}_{[0,1]}(y)\mathcal{I}_{[0,1]}(z)\mathrm{d}x\mathrm{d}y\mathrm{d}z.$$

This is a routine exercise in multiple integration.

There are many other methods to compute this integral (besides the ones found in multivariate Calculus textbooks, which typically rely on Fubini's Theorem to represent this as a sequence of three univariate integrals). The four methods described at https://stats.stackexchange.com/a/43075/919 can all be applied. I believe this responds to the various suggestions in the question about Laplace transforms, convolution integrals, and so on. The details are messy, so I will forgo any presentation of them.

It will be much simpler, however, to recognize that since $\alpha\le 1,$ (a) the indicator functions limit the integration to a unit cube; (b) because the density is constant, the integral merely computes the volume of the region of nonzero density (multiplied by the constant density value); (c) the inequality $x+y\le\alpha\le 1$ describes a right triangular prism of sides $\alpha,\alpha,1$ within that cube, whose volume therefore is $\alpha^2/2;$ and (d) from the prism a region defined by $x+y+z\le\alpha$ has been removed. This region is a pyramid with vertex at the origin and adjacent sides of lengths $\alpha,\alpha,\alpha,$ as shown by the solid mesh portion of the figure:

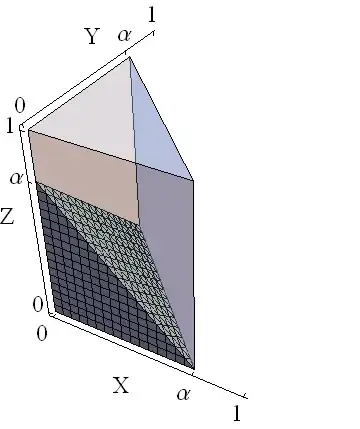
Figure

Because the pyramid's volume is $\alpha^3/6$ and for $0\le\alpha\le 1$ the probability must be the difference between the two volumes, the solution is

$$\Pr(X+Y\le\alpha \lt X+Y+Z)= \alpha^2/2 - \alpha^3/6.$$

As a check, this plot compares the preceding function (graphed in red) with estimates of the probability based on a simulation (graphed in black, surrounded by three-standard-error bands in gray):

Figure 2

The formula and simulated values are so close that they are nearly indistinguishable.

This simulation was performed in R with these commands:

n <- 1e4
sim <- matrix(runif(3*n), nrow=3)
xyz <- colSums(sim)
xy <- xyz - sim[3,]

p <- sapply(alpha <- seq(0,1,length.out=41), function(a) {
  w <- xy <= a & a <= xyz
  c(mean(w), sd(w) / sqrt(n))
})

plot(alpha, p[1,], type="l", lwd=2, col="Black", ylab="Probability")
polygon(c(alpha, rev(alpha)), 
        c(p[1,]-3*p[2,], rev(p[1,]+3*p[2,])),
        col="#00000030", border=NA)
curve(x^2/2 - x^3/6, add=TRUE, lwd=2, col="Red")
whuber
  • 281,159
  • 54
  • 637
  • 1,101