The question does not really have anything to do with the Chisquared distribution: it is about the relationship between the new ratios $X$ and $Y$ and whether that structure creates dependency. One can always easily check this oneself by generating some random values for each of the $X_i$, then generate $X$ and $Y$, and then plot $X$ vs $Y$.
Or better if you wish to think about it ...
With 2 variables:
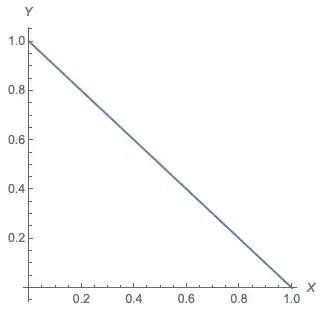
If $X = \frac{X_1}{X_1+X_2}$ and $Y = \frac{X_2}{X_1+X_2}$, then $X$ and $Y$ are two parts of the same ratio that must sum to 1 (i.e. $X+Y=1$), and the relationship between $X$ and $Y$ could be plotted as:
With 3 variables:
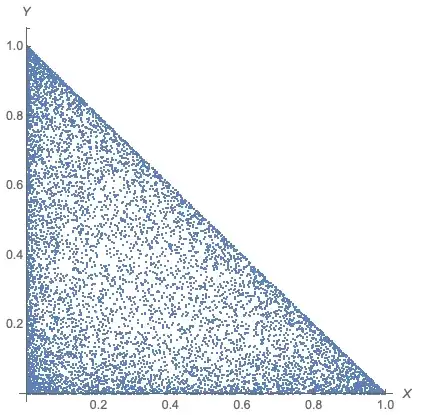
With the 3rd variable $X_3$ added, we have $X = \frac{X_1}{X_1+X_2 + X_3}$ and $Y = \frac{X_2}{X_1+X_2+X_3}$. If we define a third ratio $Z = \frac{X_3}{X_1+X_2 + X_3}$, then $X + Y + Z = 1$ (i.e. that $X + Y <1$) and thus that the domain of support for $X$ and $Y$ could be plotted as the shaded space below the line:
If you were to generate pseudorandom data for $X$ and $Y$ and plot it, it would look something like this: