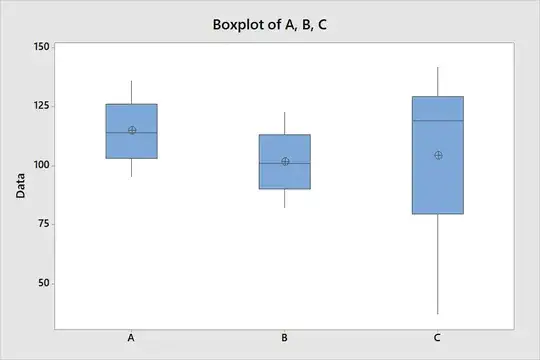
Boxplots summarize distributions to only a handful of numbers. This can be convenient when comparing many dozens of groups but with only a few groups it's better to look at all of the data.
Nevertheless, sometimes it's the only option available (such as when we have nothing but the side-by-side boxplot to look at).
In that case you have a couple of indications of the relative spreads, and several indications of skewness (or at least asymmetry).
For equality of spreads, you can compare the box-lengths,
or the range (or you might look at the distance between the whiskers if that differs from the range). Of those the box-lengths tend to be a little more robust. See also the discussion here.
Typically you're looking for a substantial difference in spread (typically a deal more than a factor of two, say) before there's much impact on tests. Of course you can avoid this issue easily by not making an assumption you're not confident in (perhaps using a Welch-Satterthwaite instead, or a more suitable parametric assumption, perhaps one where mean and variance are related, such as you get with count data).
For looking at skewness, there's an extensive discussion here about the assessment of skewness using boxplots
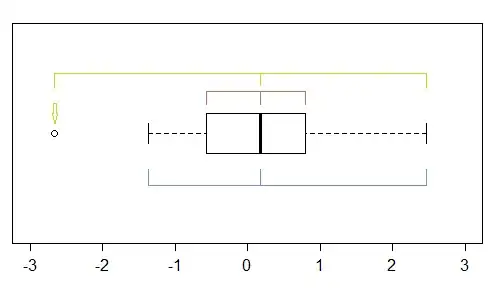
(as well as some discussion of alternative ways of considering it). In that case, you're effectively comparing the relative spread on the left and right (below and above) of the middle within each group:
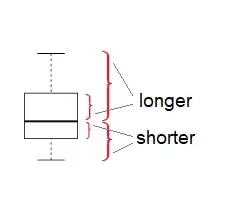
Caution is required, however, as boxplots can sometimes be quite misleading as indicators of shape. This can be seen in the four boxplots in the example at the end of the previously mentioned link.