0

I am running a generalized linear model. The dependent variable is binomial and independent variables are categorical and continuous variables. My question is : 1. Does the continuous independent variable have to be normally distributed? 2. Do I need to check for the normality of residuals of the continuous variables?

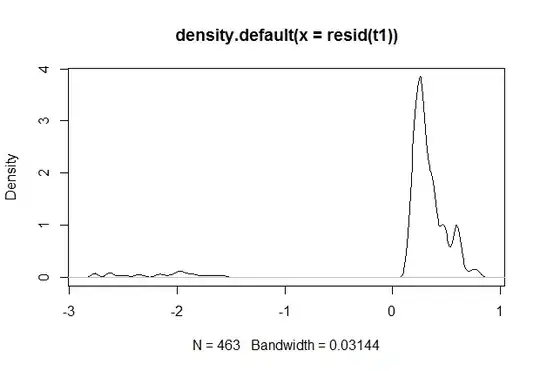
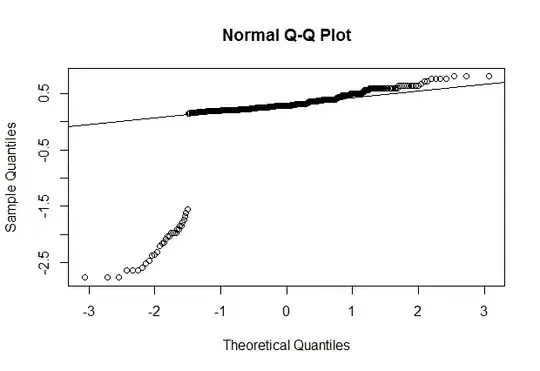
enter image description here enter image description here
These are images of the model residuals. The model is as follows.
B and A are categorical variables with two levels each and F is continuous. 

t1<-glm(B ~ A + F, family = binomial, data = d, na.action = "na.fail")
sm<-standardize(t1)
model.set<-dredge(sm)
model.set
top.model<-get.models(model.set, subset=delta<2)
top.model
#model averaging
u<-summary(model.avg(top.model), revised.var = T)
u
confint(u, full = T)
plot(density(resid(t1))) 
qqnorm(resid(t1)) 
qqline(resid(t1))

@Harlan Nelson, I have added the graphs.

Harshad
  • 61
  • 6
  • Can you let us know what your model is? – Harlan Nelson Jan 13 '19 at 03:43
  • 2
    A glm is a regression model, and **do not make any distribvutional assumptions about the predictors/independent variables**. – kjetil b halvorsen Jan 13 '19 at 13:54
  • @Harlan Nelson. Here B and A are categorical with two levels, F is continuous. – Harshad Jan 14 '19 at 14:38
  • 1
    If your model states that they are normal then they should be. If the model assumes that they are just fixed values, then there really is no distribution. Many GLM models, and yours it seems, only require that some transformation of the error term to be normal. It is possible to write models in any way you want. – Harlan Nelson Feb 01 '19 at 16:28

0 Answers0