1

I have this dataset: ds

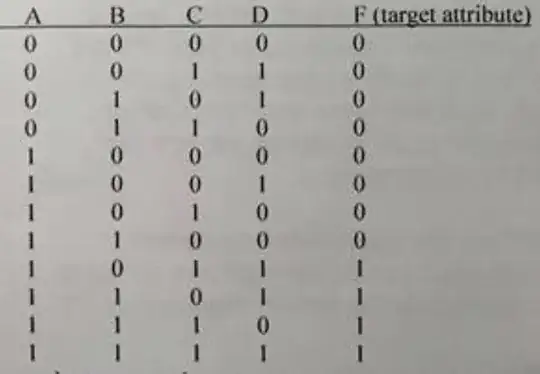
I want to know if it is linearly separable (fully separable).

I want to use this rule, but I'm not sure if it's correct:

Make $X'$ - matrix with d+1 column of all 1's. Then using Gauss-Jordan elimination, and if I get a solution - the data is linearly separable. Else - the data is not linearly separable.

I understood it from this presentation: rule

Using matrix calculations I got that this system is inconsistent $=>$ not linearly separable.

Is this true? This data is linearly separable? The rule I'm using is ok?

Ferdi
  • 4,882
  • 7
  • 42
  • 62
JohnSnowTheDeveloper
  • 145
  • 1
  • 7
  • 1
    Try to formulate it as a problem in linear programming. You could get some ideas from [here](https://stats.stackexchange.com/questions/11109/how-to-deal-with-perfect-separation-in-logistic-regression) or similar posts. – kjetil b halvorsen Jan 08 '19 at 23:00
  • I think you have misunderstood linear separability. take 1d. A = [-1, -2, -3, 1, 2, 3] and F = [0, 0, 0, 1, 1, 1]. then this is linearly separable, but there is no W that gives you F (so no solution to matrix equation) .... you threshold the matrix multiplication to get F ... – seanv507 Jan 09 '19 at 00:31
  • 3
    That the system itself isn't perfectly collinear doesn't mean it's not linearly separable. (This one is actually doable by inspection. Look at the sum of the predictors.) – Glen_b Jan 09 '19 at 00:34
  • I understand that if X is not perfectly collinear it doesn"t mean it's not linearly seperable, but what about X'? After adding column of ones? For making a linear predictor without a bias... – JohnSnowTheDeveloper Jan 09 '19 at 08:07

1 Answers1

1

The photograph of the question suggests to me that this is either a test or a textbook question. These kinds of questions are designed to be answered quickly, not necessarily thoroughly.

Consider $X=[A, B, C, D]$ a matrix composed of column vectors $A, B, C, D$ from the picture. By inspection, $X\mathbf{1}=\hat{y}=[0,2,2,2,1,2,2,2,3,3,3,4]^\top$ separates the labels using a rule such as $\text{if }\hat{y}>2.5 \text{ then } 1 \text{ else } 0$. This is linear separation.

These facts are all you need.

Of course there are many such rules and many choices of weights for which we can show the linear separability. But determining whether or not there is linear separability doesn't require you to characterize all of the possible solutions, just show that at least one linear separation exists.

Sycorax
  • 76,417
  • 20
  • 189
  • 313