Why log-transform to normal distribution for decision trees?

Question

On page 304 of chapter 8 of An Introduction to Statistical Learning with Applications in R (James et al.), the authors say:

We use the Hitters data set to predict a baseball player’s Salary based on Years (the number of years that he has played in the major leagues) and Hits (the number of hits that he made in the previous year). We first remove observations that are missing Salary values, and log-transform Salary so that its distribution has more of a typical bell-shape. (Recall that Salary is measured in thousands of dollars.)

No additional motivation for the log-transform is given. Being that the data are being fed into decision tree algorithms, why was it important to force the data into a normal distribution? I thought most/all decision tree algorithms were invariant to scale changes.

Answer 1

In this case, the salary is the target (dependent variable/outcome) of the decision tree, not one of the features (independent variables/predictors). You are correct that decision trees are insensitive to the scale of the predictors, but since I suspect there are a small number of extremely large salaries, transforming the salaries might improve predictions because loss functions which minimize square error will not be so strongly influenced by these large values.

Answer 2

I downloaded last year's salaries. It is very likely they follow a Pareto distribution. The histogram is shown below.

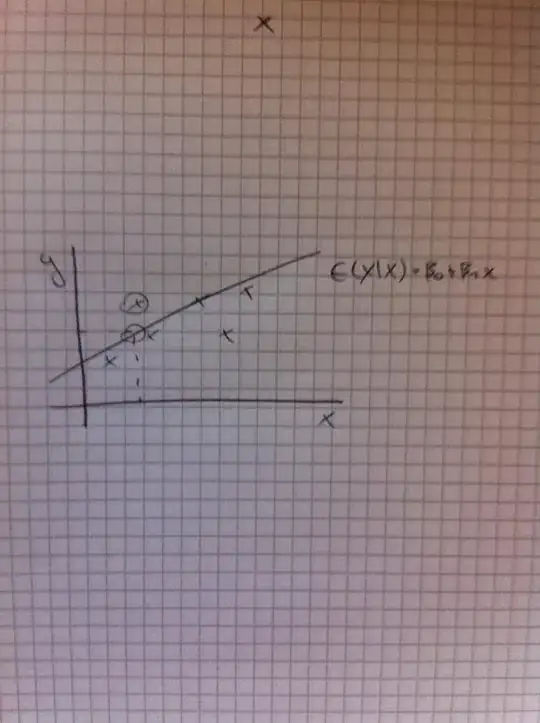
The pdf of the Pareto distribution is $$\frac{\alpha{x_m}^\alpha}{x^{\alpha+1}}.$$

The scale parameter $x_m$ is \$545,000, the lowest salary last year. I estimated the shape parameter, $\alpha$, as 0.7848238 using MLE. This matters because when $\alpha<2,$ then the distribution has no variance. More properly, its variance is undefined. If any of your variables lacks a mean or a variance, then you cannot use anything that minimizes squared loss.

The distribution of the log of the variables does have a variance and so you can use least squares style methodologies on them. This is actually a serious omission from your textbook. Some things, like the stock market returns which have neither a mean nor a variance, or baseball salaries, which lack a variance will make OLS models meaningless. The log is not, inherently, the best treatment, but it does work.

Taking the log does not give you a bell shape.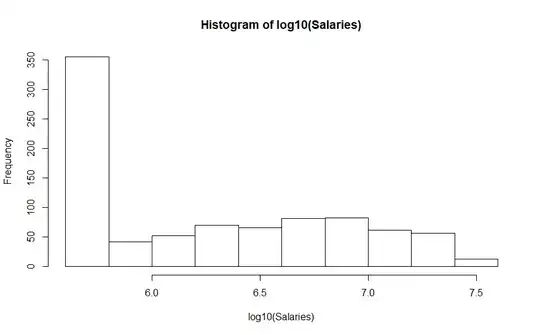

This is entirely about being certain that all of your data has a variance. If all of the assumptions for OLS are met, then the underlying distributions do not matter. They can be insane looking, but variance has to be defined everywhere.

EDIT As Therkel pointed out in the comments when $\alpha<1$ then no mean exists either. There is a comment by Cliff AB that I should take up as well. He argues that the distribution is doubly bounded and so a finite variance and mean exist. I would disagree with that as an economist. It is true that there is only so much wealth in the world, but it is also true that we have no idea what it is. Furthermore, that wealth is changing every second of every day as people make individual choices.

The worker who does not pick that one apple reduces wealth if that apple is never picked and reduces available wealth regardless. An apple on a tree has no income value until it picked and processed. This makes the right-hand side constraint stochastic. For the purposes of baseball, the stochastic effect should be considered to be zero.

Baseball, as a percentage of world output, is so miniscule that you could ignore it. The same is true for American football, North American hockey, or for that matter, live stage theater for the whole United States.

The fact that you can model this data with a Pareto distribution means you have no mean or variance if the estimates are valid. If you take the log, you end up with finite variance. If you divide the data by its minimum value and take the logs, you end up with the exponential distribution, which is well enough behaved, but then you get interpretation problems.