0

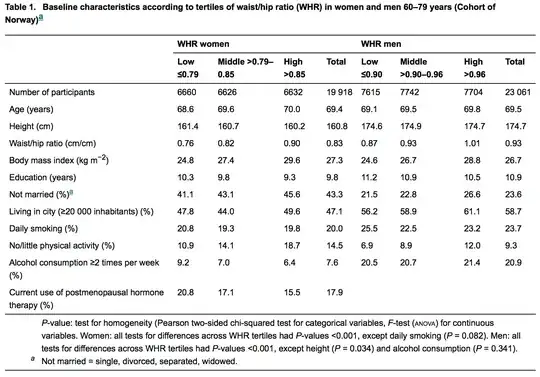
I want to the derive the PDF which looks like the sum of a triangular and uniform distribution which looks like this:

enter image description here

To do this I have simply added the PDFs for the rectangular and triangular parts, over the range $[n,N].$

A triangular distribution, with these bounds, has the following PDF:

$$f(x) = \frac{2(N-x)}{(N-n)^2}$$

The scaled uniform distribution has the following PDF:

$$g(x) = \frac{1}{N-n}$$

Then (I believe), the compound distribution is simply:

$$h(x) := f(x) + g(x) = \frac{3N -2x -n}{(N-n)^2}$$

However, I do get a bit confused here, since this distribution needs to be normalised, which is simply done as so:

$$h_{\text{norm}}(x) = \frac{1}{\int_x h(x)} h(x)$$

Does this seem reasonable, or am I wildly off-chart here?

This is a related question but it seems very complicated, for what should be quite simple.

Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161
Astrid
  • 745
  • 7
  • 17
  • Could you explain what you mean by a "compound pdf"? What is it intended to represent? Your picture is puzzling because the areas of the square and triangle differ, demonstrating their graphs cannot both represent densities. – whuber Dec 29 '18 at 18:17
  • The compound part is the combination of the square and the triangle. Imagine that you know the PDF of each individual geometry and you would like to find an expression for the combination of both PDFs, that is what I mean by _compound_. I am studying a problem which gives rise to a histogram of this shape, this is the reason for me wanting to find an analytical expression for the distribution. – Astrid Dec 29 '18 at 21:43
  • Could you explain what "the PDF of [an] individual geometry" might possibly mean? And exactly how one "combines" two PDFs (and how that would be interpreted)? I am concerned that your question might ultimately be based on a misunderstanding of what these terms mean in a particular application. If the concern merely is of a histogram of this shape, then that is thoroughly addressed in the related question you identified, suggesting your interest is a little broader (or different) than that. – whuber Dec 29 '18 at 22:56
  • It is fully possible that I have misunderstood it. Though @jbowman has provided a result below which is what I was broadly looking for. The derived result below is also less complex than the one I linked. When I say the PDF of an individual geometry it could be e.g. the triangular distribution (PDF of a triangle) or a trapezoidal distribution (PDF of a trapezium). I also fully admit that I may have abused terminology here and would be happy to be corrected. Ultimately I was just interested in finding the PDF of the area under the sloped line in the above figure. – Astrid Dec 29 '18 at 23:00
  • @Astrid could you clarify whether you mean [compound distribution](https://en.wikipedia.org/wiki/Compound_probability_distribution) or [mixture distribution](https://en.wikipedia.org/wiki/Mixture_distribution). Also, is the expression for the triangular distribution (which is more like a trapezium) what you want? – Sextus Empiricus Jan 18 '19 at 09:33
  • I do not mean a mixture distribution (as far as I understand the concept), but I mean the distribution as seen in the above image where, for reasons of exposition, we can think of the PMF as the area under the geometrical shape that results from stacking a triangle on top of a square. – Astrid Jan 18 '19 at 09:35

2 Answers2

1

The first step is to find an equation for the unnormalized density function, which in this case is the line at the top of your graph:

$$f(x) \propto 9 - {4(x-n) \over N-n}$$

We then integrate this over the range $[n,N]$ to find the constant of integration $c$:

$$c = \left(9 + {4n \over N-n}\right)\int_n^Ndx \quad - \quad {4 \over N-n}\int_n^Nxdx$$

Working through the integrals gets us to:

$$c = 9N - 9n + 4n -2(N-n)$$

which simplifies to $c=7N-3n$. Combining this with our unnormalized density function and rearranging terms leads to:

$$f(x) = {9N - 5n -4x \over (7N - 3n)(N-n)}$$

jbowman
  • 31,550
  • 8
  • 54
  • 107
  • For clarity; the result $f(x)$ is not a proper density since it is not normalised yet? I.e. finding the constant of integration does not automatically yield us a normalised density. Further, I calculate the slope as $m=\frac{5-9}{N-n}$ but you have somehow got an extra $-n$ in there -- where did it come from? Also thanks, this is great. – Astrid Dec 29 '18 at 22:05
  • 1
    1. The final result is normalized, as we divided by $(7N-3n)$, the constant of integration. 2. The slope isn't all we want; we want the value of $f(x)$ for each $x$, and that requires knowing the intercept too. You'll observe that the slope as I have it is $-4/(N-n)$, the same as what you have found, but the intercept does depend on $n$, and that's where the extra $4n/(N-n)$ comes from. – jbowman Dec 29 '18 at 22:35
  • jbowman, to get the CDF of this expression I simply integrate $f(x) = {9N - 5n -4x \over (7N - 3n)(N-n)}$ once if I have understood the process correctly? – Astrid Dec 30 '18 at 15:16
  • 1
    That's right, and expected values etc. are done similarly. – jbowman Dec 30 '18 at 15:26
  • @jbowman It disturbed me how this outcome was different from mine. I see now where the difference is. You evaluated $\int_n^N x dx = \frac{1}{2} (N-n)^2$ missing a part $n(N-n)$. Then this will add an extra term $-4n$ and it should be $c=7N-7n$ instead of $c=7N-3n$ – Sextus Empiricus Jan 18 '19 at 11:04
  • @MartijnWeterings - I'll check my math for sure, but ATM it looks to me like I have the $n(N-n)$ in the first term of the integration. Maybe I messed up, though. – jbowman Jan 18 '19 at 17:06
1

Your image shows the sum of two functions which relates to a mixture distribution:

$$h(x) = a g(x) + (1-a) f(x)$$

(see also this discussion)

with

  • the continuous distribution:

    $$g(x) = \begin{cases} \frac{1}{N-n} & \quad \text{ for $ n \leq x\leq$ N } \\ 0 & \quad \text{otherwise}\end{cases}$$

  • a triangular distribution:

    $$f(x) = \begin{cases} 2 \frac{N-x}{(N-n)^2} & \quad \text{ for $ n \leq x\leq$ N } \\ 0 & \quad \text{otherwise}\end{cases}$$

You do not need to worry about the constant of integration since:

$$\begin{array}{rcl} \int_n^N h(x)dx &=& \int_n^N \underbrace{( a g(x) + (1-a) f(x))}_{=h(x)} dx \\ & = & \int_n^N a g(x) dx + \int_n^N (1-a) f(x) dx \\ & = & a \underbrace{\int_n^N g(x) dx}_{=1} + (1-a) \underbrace{\int_n^N f(x) dx}_{=1} \\ & = & a + (1-a) = 1 \end{array} $$

To get your figure you need to add 5/7 times the uniform (rectangular) distribution and 2/7 times the triangle distribution.

example

$$h(x) = \frac{5}{7} g(x) + \frac{2}{7} f(x) = \begin{cases} \frac{\frac{5}{7} + \frac{4}{7} \frac{N-x}{N-n} }{N-n} & \quad \text{ for $ n \leq x\leq$ N } \\ 0 & \quad \text{otherwise}\end{cases}$$

Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161