28

In a recent paper , Masicampo and Lalande (M-L) collected a large number of p-values published in many different studies. They observed a curious jump in the histogram of the p-values right at the canonical critical level of 5%.

There is a nice discussion about this M-L Phenomena on Prof. Wasserman's blog:

http://normaldeviate.wordpress.com/2012/08/16/p-values-gone-wild-and-multiscale-madness/

On his blog, you will find the histogram:

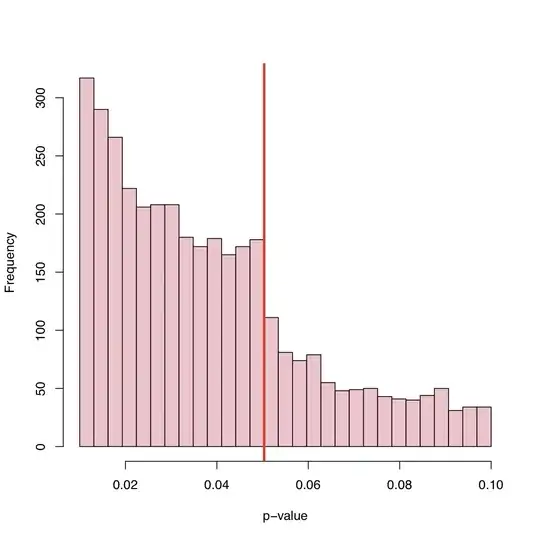
Histogram of published p-values

Since the 5% level is a convention and not a law of nature, what causes this behavior of the empirical distribution of published p-values?

Selection bias, systematic "adjustment" of p-values just above the canonical critical level, or what?

Jeromy Anglim
  • 42,044
  • 23
  • 146
  • 250
Zen
  • 21,786
  • 3
  • 72
  • 114
  • 11
    There are at least 2 sorts of explanation: 1) the "file drawer problem" - studies with p < .05 get published, those above don't, so it's really a mixture of two distributions 2) People are manipulating things, possibly subconciously, to get p < .05 – Peter Flom Oct 01 '12 at 17:51
  • 3
    Hi @Zen . Yes, exactly that sort of thing. There is a strong tendency to do stuff like this. If our theory is confirmed, we are less likely to go look for statistical problems than if it is not. This seems to be part of our nature, but it is something to try to guard against. – Peter Flom Oct 01 '12 at 17:57
  • @Zen You might be interested in this post on Andrew Gelman's blog that mentions some research that finds that there's no publication bias in research about publication bias...! http://andrewgelman.com/2012/04/systematic-review-of-publication-bias-in-studies-on-publication-bias/ – smillig Oct 01 '12 at 18:51
  • 1
    What would be interesting is the back-calculate the p-values from papers in journals that expressly reject p-value based papers, like *Epidemiology* used to (and in some senses, still does). I wonder if it changes if the journal has out and out stated it doesn't care, or if reviewers/authors are still doing mental ad-hoc testing based on confidence intervals. – Fomite Oct 01 '12 at 23:11
  • @PeterFlom: I attribute it to the "file drawer" and to fudging data to get the results they want, but I think your suggestion of "if it ain't broke, don't fix it" is a good explanation that avoids malfeasance. People should be as eager to find holes in their successful argument as to find loopholes for their unsuccessful argument, ala Feynman, but... – Wayne Oct 02 '12 at 00:43
  • 4
    As explained on Larry's blog, this is a collection of published p-values, rather than a random sample of p-values sampled from the World of p-values. There is thus no reason a uniform distribution should appear in the picture, even as part of a mixture as modelled in Larry's post. – Xi'an Oct 02 '12 at 05:26

3 Answers3

14

(1) As already mentioned by @PeterFlom, one explanation might be related to the "file drawer" problem. (2) @Zen also mentioned the case where the author(s) manipulate(s) the data or the models (e.g. data dredging). (3) However, we do not test hypotheses on a purely random basis. That is, hypotheses are not chosen by chance but we have (more or less strong) theoretical assumption.

You also might be interested in the works of Gerber and Malhotra who recently have conducted research in that area applying the so called "caliper test":

You also might be interested in this special issue edited by Andreas Diekmann:

Michael R. Chernick
  • 39,640
  • 28
  • 74
  • 143
Bernd Weiss
  • 7,044
  • 28
  • 40
10

One argument that is missing so far is the flexibility of data analysis known as researchers degrees of freedom. In every analysis there are many decisions to be made, where to set the outlier criterion, how to transform the data, and ...

This was recently raised in an influential article by Simmons, Nelson and Simonsohn:

Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2011). False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant. Psychological Science, 22(11), 1359 –1366. doi:10.1177/0956797611417632

(Note that this is the same Simonsohn responsible for some recently detected cases of data fraud in Social Psychology, e.g., interview, blog-post)

Henrik
  • 13,314
  • 9
  • 63
  • 123
8

I think it is a combination of everything that has already been said. This is very interesting data and I have not thought of looking at p-value distributions like this before. If the null hypothesis is true the p-value would be uniform. But of course with published results we would not see uniformity for many reasons.

  1. We do the study because we expect the null hypothesis to be false. So we should get significant results more often than not.

  2. If the null hypothesis were false only half the time we would not get a uniform distribution of p-values.

  3. File drawer problem: As mentioned we would be afraid to submit the paper when the p-value is not significant e.g. below 0.05.

  4. Publishers will reject the paper because of non-signifcant results even though we chose to submit it.

  5. When the results are on the borderline we will do things (maybe not with malicious intent) to get significance. (a) round down to 0.05 when the p-value is 0.053, (b) find observations that we think might be outliers and after rmoving them the p-value drops below 0.05.

I hope this summarizes everything that has been said in a reasonably understandable way.

What I think is interest is that we see p-values between 0.05 and 0.1. If publication rules were to reject anything with p-values above 0.05 then the right tail would cut off at 0.05. Did it actually cutoff at 0.10? if so maybe some authors and some journals will accept a significance level of 0.10 but nothing higher.

Since many papers include several p-values (adjusted for multiplcity or not) and the paper is accepted because the key tests were significant we might see nonsignificant p-values included on the list. This raises the question "Were all reported p-values in the paper included in the histogram?"

One additional observation is that there is a significant trend upward in the frequency of published papers as the p-value gets far below 0.05. Maybe that is an indication of authors overinterpreting the p-value thinking p<0.0001 is much more worthy of publication. I think author ignore or don't realize that the p-value depends as much on sample size as it does on the magnitude of the effect size.

Michael R. Chernick
  • 39,640
  • 28
  • 74
  • 143