0

The price of an option (in finance) is given by the famous Black-Scholes equation. I would like to design a neural network to predict the price of an option. Basically the inputs are the attributes of the option and the output is the price. So we are essentially learning a deterministic non-linear function.

My issue is that the in sample average mean-sqaured-error is not low enough for my purposes. I know that the issue is a bias problem since the in sample error is too high. Moreover, the in sample and out of sample error are very similar.

I've replicated the results in this paper: https://srdas.github.io/Papers/BlackScholesNN.pdf

Now I am trying to optimize the network they present in the paper. They leave network optimization for further work in their paper.

Basically, I don't have any intuition for which network architecture to use. I have tried a few obvious things like increasing the number of layers, number of nodes per layer, different activation functions, but it doesn't seem to help much.

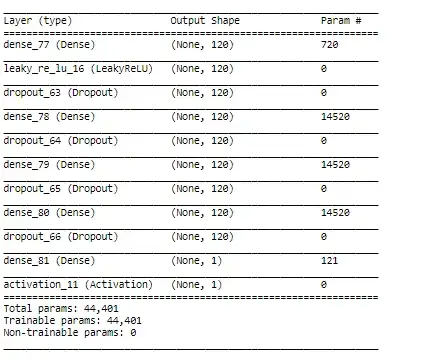
In their paper, they use this architecture:

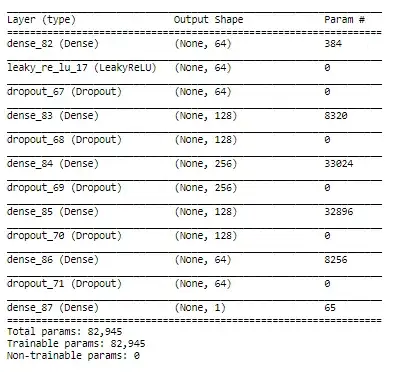
enter image description here

I've been dabbling with different networks. For example, I tried this: enter image description here

But it doesn't seem to help.

What is the intuition for next steps? Should I play around with my features (i.e. normalization or something else)? How do I optimize the network without just trying random things?

EDIT: Optimize means reduce of out of sample loss.

John Doe
  • 113
  • 4
  • You might also be interested in the (growing) literature base that specifically focuses on NNs for differential equations. One example: https://arxiv.org/pdf/1806.07366.pdf (although this particular paper focuses on ODEs whereas Black-Scholes is a PDE, there is still a literature base dedicated to these topics) – Sycorax Dec 20 '18 at 17:38
  • It would help if you could clarify what you mean by "Now I am trying to optimize the network they present in the paper. They leave network optimization for further work in their paper." What are you trying to optimize? Are you trying to improve the precision of the network's outputs? Are you trying to make the model train more quickly? Are you trying to reduce the number of parameters required to achieve a certain level of precision? Something else? – Sycorax Dec 20 '18 at 21:40
  • @Sycorax precision of outputs. Minimize out of sample error. – John Doe Dec 20 '18 at 21:49
  • Have you reviewed the answers at https://stats.stackexchange.com/questions/365778/what-should-i-do-when-my-neural-network-doesnt-generalize-well ? What have you tried? What results did you find when you implemented these recommendations? – Sycorax Dec 20 '18 at 22:05
  • @Sycorax I tried a few of those things. I seem to have a bias problem, not an over-fitting issue. – John Doe Dec 21 '18 at 16:24
  • Can you edit your post to include information about what the bias problem is, how you're measuring it, and what your desired result is? – Sycorax Dec 21 '18 at 16:25
  • @Sycorax I did that – John Doe Dec 21 '18 at 16:28

0 Answers0