9

The summarized version of my question

(26th December 2018)

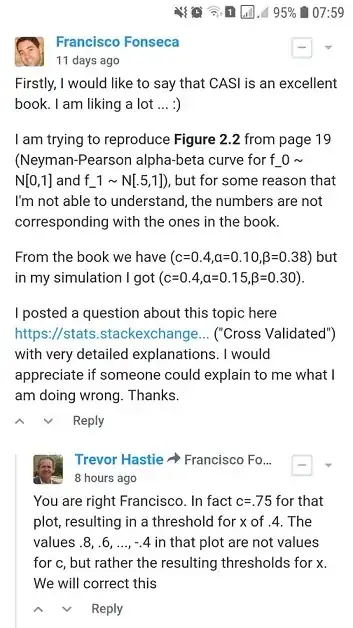
I am trying to reproduce Figure 2.2 from Computer Age Statistical Inference by Efron and Hastie, but for some reason that I'm not able to understand, the numbers are not corresponding with the ones in the book.

Assume we are trying to decide between two possible probability density functions for the observed data $x$, a null hypothesis density $f_0\left(x\right)$ and an alternative density $f_1\left(x\right)$. A testing rule $t\left(x\right)$ says which choice, $0$ or $1$, we will make having observed data $x$. Any such rule has two associated frequentist error probabilities: choosing $f_1$ when actually $f_0$ generated $x$, and vice versa,

$$ \alpha = \text{Pr}_{f_0} \{t(x)=1\}, $$ $$ \beta = \text{Pr}_{f_1} \{t(x)=0\}. $$

Let $L(x)$ be the likelihood ratio,

$$ L(x) = \frac{f_1\left(x\right)}{f_0\left(x\right)} $$

So, the Neyman–Pearson lemma says that the testing rule of the form $t_c(x)$ is the optimum hypothesis-testing algorithm

$$ t_c(x) = \left\{ \begin{array}{ll} 1\enspace\text{if log } L(x) \ge c\\ 0\enspace\text{if log } L(x) \lt c.\end{array} \right. $$

For $f_0 \sim \mathcal{N} \left(0,1\right), \enspace f_1 \sim \mathcal{N} \left(0.5,1\right)$, and sample size $n=10$ what would be the values for $\alpha$ and $\beta$ for a cutoff $c=0.4$?

  • From Figure 2.2 of Computer Age Statistical Inference by Efron and Hastie we have:
    • $\alpha=0.10$ and $\beta=0.38$ for a cutoff $c=0.4$
  • I found $\alpha=0.15$ and $\beta=0.30$ for a cutoff $c=0.4$ using two different approaches: A) simulation and B) analytically.

I would appreciate if someone could explain to me how to obtain $\alpha=0.10$ and $\beta=0.38$ for a cutoff $c=0.4$. Thanks.

The summarized version of my question finishes here. From now you will find:

  • In section A) details and complete python code of my simulation approach.
  • In section B) details and complete python code of the analytically approach.

A) My simulation approach with complete python code and explanations

(20th December 2018)

From the book ...

In the same spirit, the Neyman–Pearson lemma provides an optimum hypothesis-testing algorithm. This is perhaps the most elegant of frequentist constructions. In its simplest formulation, the NP lemma assumes we are trying to decide between two possible probability density functions for the observed data $x$, a null hypothesis density $f_0\left(x\right)$ and an alternative density $f_1\left(x\right)$. A testing rule $t\left(x\right)$ says which choice, $0$ or $1$, we will make having observed data $x$. Any such rule has two associated frequentist error probabilities: choosing $f_1$ when actually $f_0$ generated $x$, and vice versa,

$$ \alpha = \text{Pr}_{f_0} \{t(x)=1\}, $$ $$ \beta = \text{Pr}_{f_1} \{t(x)=0\}. $$

Let $L(x)$ be the likelihood ratio,

$$ L(x) = \frac{f_1\left(x\right)}{f_0\left(x\right)} $$

(Source: Efron, B., & Hastie, T. (2016). Computer Age Statistical Inference: Algorithms, Evidence, and Data Science. Cambridge: Cambridge University Press.)

So, I implemented the python code below ...

import numpy as np

def likelihood_ratio(x, f1_density, f0_density):
    return np.prod(f1_density.pdf(x)) / np.prod(f0_density.pdf(x))

Again, from the book ...

and define the testing rule $t_c(x)$ by

$$ t_c(x) = \left\{ \begin{array}{ll} 1\enspace\text{if log } L(x) \ge c\\ 0\enspace\text{if log } L(x) \lt c.\end{array} \right. $$

(Source: Efron, B., & Hastie, T. (2016). Computer Age Statistical Inference: Algorithms, Evidence, and Data Science. Cambridge: Cambridge University Press.)

So, I implemented the python code below ...

def Neyman_Pearson_testing_rule(x, cutoff, f0_density, f1_density):
    lr = likelihood_ratio(x, f1_density, f0_density)
    llr = np.log(lr)
    
    if llr >= cutoff:
        return 1
    else:
        return 0

Finally, from the book ...

enter image description here

Where it is possible to conclude that a cutoff $c=0.4$ will imply $\alpha=0.10$ and $\beta=0.38$.

So, I implemented the python code below ...

def alpha_simulation(cutoff, f0_density, f1_density, sample_size, replicates):
    NP_test_results = []
    
    for _ in range(replicates):
        x = f0_density.rvs(size=sample_size)
        test = Neyman_Pearson_testing_rule(x, cutoff, f0_density, f1_density)
        NP_test_results.append(test)
    
    return np.sum(NP_test_results) / float(replicates)

def beta_simulation(cutoff, f0_density, f1_density, sample_size, replicates):
    NP_test_results = []
    
    for _ in range(replicates):
        x = f1_density.rvs(size=sample_size)
        test = Neyman_Pearson_testing_rule(x, cutoff, f0_density, f1_density)
        NP_test_results.append(test)
    
    return (replicates - np.sum(NP_test_results)) / float(replicates)

and the code ...

from scipy import stats as st
    
f0_density = st.norm(loc=0, scale=1)
f1_density = st.norm(loc=0.5, scale=1)

sample_size = 10
replicates = 12000

cutoffs = []
alphas_simulated = []
betas_simulated = []
for cutoff in np.arange(3.2, -3.6, -0.4):
    alpha_ = alpha_simulation(cutoff, f0_density, f1_density, sample_size, replicates)
    beta_ = beta_simulation(cutoff, f0_density, f1_density, sample_size, replicates)
    
    cutoffs.append(cutoff)
    alphas_simulated.append(alpha_)
    betas_simulated.append(beta_)

and the code ...

import matplotlib.pyplot as plt
%matplotlib inline

# Reproducing Figure 2.2 from simulation results.
plt.xlabel('$\\alpha$')
plt.ylabel('$\\beta$')
plt.xlim(-0.1, 1.05)
plt.ylim(-0.1, 1.05)
plt.axvline(x=0, color='b', linestyle='--')
plt.axvline(x=1, color='b', linestyle='--')
plt.axhline(y=0, color='b', linestyle='--')
plt.axhline(y=1, color='b', linestyle='--')
figure_2_2 = plt.plot(alphas_simulated, betas_simulated, 'ro', alphas_simulated, betas_simulated, 'k-')

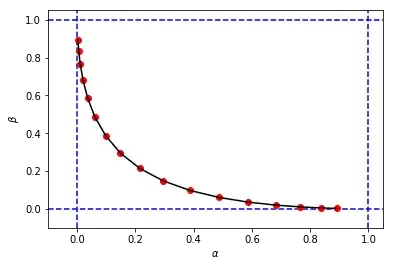
to obtain something like this:

enter image description here

that looks similar to the original figure from the book, but the 3-tuples $(c,\alpha,\beta)$ from my simulation has different values of $\alpha$ and $\beta$ when compared with the ones of the book for the same cutoff $c$. For example:

  • from the book we have $(c=0.4, \alpha=0.10, \beta=0.38)$
  • from my simulation we have:
    • $(c=0.4, \alpha=0.15, \beta=0.30)$
    • $(c=0.8, \alpha=0.10, \beta=0.39)$

It seems that the cutoff $c=0.8$ from my simulation is equivalent with the cutoff $c=0.4$ from the book.

I would appreciate if someone could explain to me what I am doing wrong here. Thanks.

B) My calculation approach with complete python code and explanations

(26th December 2018)

Still trying to understand the difference between the results of my simulation (alpha_simulation(.), beta_simulation(.)) and those presented in the book, with the help of a statistician (Sofia) friend of mine, we calculated $\alpha$ and $\beta$ analytically instead of via simulation, so ...

Once that

$$ f_0 \sim \mathcal{N} \left(0,1\right) $$ $$ f_1 \sim \mathcal{N} \left(0.5,1\right) $$

then

$$ f\left(x \;\middle\vert\; \mu, \sigma^2 \right) = \prod_{i = 1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left(x_i-\mu\right)^2}{2\sigma^2}} $$

Moreover,

$$ L(x) = \frac{f_1\left(x\right)}{f_0\left(x\right)} $$

so,

$$ L(x) = \frac{f_1\left(x\;\middle\vert\; \mu_1, \sigma^2\right)}{f_0\left(x\;\middle\vert\; \mu_0, \sigma^2\right)} = \frac{\prod_{i = 1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left(x_i-\mu_1\right)^2}{2\sigma^2}}}{\prod_{i = 1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left(x_i-\mu_0\right)^2}{2\sigma^2}}} $$

Therefore, by performing some algebraic simplifications (as below), we will have:

$$ L(x) = \frac{\left(\frac{1}{\sqrt{2\pi\sigma^2}}\right)^n e^{-\frac{\sum_{i = 1}^{n} \left(x_i-\mu_1\right)^2}{2\sigma^2}}}{\left(\frac{1}{\sqrt{2\pi\sigma^2}}\right)^n e^{-\frac{\sum_{i = 1}^{n} \left(x_i-\mu_0\right)^2}{2\sigma^2}}} $$

$$ = e^{\frac{-\sum_{i = 1}^{n} \left(x_i-\mu_1\right)^2 + \sum_{i = 1}^{n} \left(x_i-\mu_0\right)^2}{2\sigma^2}} $$

$$ = e^{\frac{-\sum_{i = 1}^{n} \left(x_i^2 -2x_i\mu_1 + \mu_1^2\right) + \sum_{i = 1}^{n} \left(x_i^2 -2x_i\mu_0 + \mu_0^2\right)}{2\sigma^2}} $$

$$ = e^{\frac{-\sum_{i = 1}^{n}x_i^2 + 2\mu_1\sum_{i = 1}^{n}x_i - \sum_{i = 1}^{n}\mu_1^2 + \sum_{i = 1}^{n}x_i^2 - 2\mu_0\sum_{i = 1}^{n}x_i + \sum_{i = 1}^{n}\mu_0^2}{2\sigma^2}} $$

$$ = e^{\frac{2\left(\mu_1-\mu_0\right)\sum_{i = 1}^{n}x_i + n\left(\mu_0^2-\mu_1^2\right)}{2\sigma^2}} $$.

So, if

$$ t_c(x) = \left\{ \begin{array}{ll} 1\enspace\text{if log } L(x) \ge c\\ 0\enspace\text{if log } L(x) \lt c.\end{array} \right. $$

then, for $\text{log } L(x) \ge c$ we will have:

$$ \text{log } \left( e^{\frac{2\left(\mu_1-\mu_0\right)\sum_{i = 1}^{n}x_i + n\left(\mu_0^2-\mu_1^2\right)}{2\sigma^2}} \right) \ge c $$

$$ \frac{2\left(\mu_1-\mu_0\right)\sum_{i = 1}^{n}x_i + n\left(\mu_0^2-\mu_1^2\right)}{2\sigma^2} \ge c $$

$$ \sum_{i = 1}^{n}x_i \ge \frac{2c\sigma^2 - n\left(\mu_0^2-\mu_1^2\right)}{2\left(\mu_1-\mu_0\right)} $$

$$ \sum_{i = 1}^{n}x_i \ge \frac{2c\sigma^2}{2\left(\mu_1-\mu_0\right)} - \frac{n\left(\mu_0^2-\mu_1^2\right)}{2\left(\mu_1-\mu_0\right)} $$

$$ \sum_{i = 1}^{n}x_i \ge \frac{c\sigma^2}{\left(\mu_1-\mu_0\right)} - \frac{n\left(\mu_0^2-\mu_1^2\right)}{2\left(\mu_1-\mu_0\right)} $$

$$ \sum_{i = 1}^{n}x_i \ge \frac{c\sigma^2}{\left(\mu_1-\mu_0\right)} + \frac{n\left(\mu_1^2-\mu_0^2\right)}{2\left(\mu_1-\mu_0\right)} $$

$$ \sum_{i = 1}^{n}x_i \ge \frac{c\sigma^2}{\left(\mu_1-\mu_0\right)} + \frac{n\left(\mu_1-\mu_0\right)\left(\mu_1+\mu_0\right)}{2\left(\mu_1-\mu_0\right)} $$

$$ \sum_{i = 1}^{n}x_i \ge \frac{c\sigma^2}{\left(\mu_1-\mu_0\right)} + \frac{n\left(\mu_1+\mu_0\right)}{2} $$

$$ \left(\frac{1}{n}\right) \sum_{i = 1}^{n}x_i \ge \left(\frac{1}{n}\right) \left( \frac{c\sigma^2}{\left(\mu_1-\mu_0\right)} + \frac{n\left(\mu_1+\mu_0\right)}{2}\right) $$

$$ \frac{\sum_{i = 1}^{n}x_i}{n} \ge \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

$$ \bar{x} \ge \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

$$ \bar{x} \ge k \text{, where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

resulting in

$$ t_c(x) = \left\{ \begin{array}{ll} 1\enspace\text{if } \bar{x} \ge k\\ 0\enspace\text{if } \bar{x} \lt k.\end{array} \right. \enspace \enspace \text{, where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

In order to calculate $\alpha$ and $\beta$, we know that:

$$ \alpha = \text{Pr}_{f_0} \{t(x)=1\}, $$ $$ \beta = \text{Pr}_{f_1} \{t(x)=0\}. $$

so,

$$ \begin{array}{ll} \alpha = \text{Pr}_{f_0} \{\bar{x} \ge k\},\\ \beta = \text{Pr}_{f_1} \{\bar{x} \lt k\}.\end{array} \enspace \enspace \text{ where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

For $\alpha$ ...

$$ \alpha = \text{Pr}_{f_0} \{\bar{x} \ge k\} = \text{Pr}_{f_0} \{\bar{x} - \mu_0 \ge k - \mu_0\} $$

$$ \alpha = \text{Pr}_{f_0} \left\{\frac{\bar{x} - \mu_0}{\frac{\sigma}{\sqrt{n}}} \ge \frac{k - \mu_0}{\frac{\sigma}{\sqrt{n}}}\right\} $$

$$ \alpha = \text{Pr}_{f_0} \left\{\text{z-score} \ge \frac{k - \mu_0}{\frac{\sigma}{\sqrt{n}}}\right\} \enspace \enspace \text{ where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

so, I implemented the python code below:

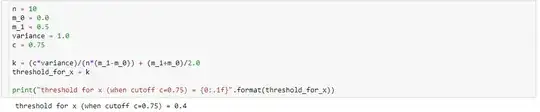
def alpha_calculation(cutoff, m_0, m_1, variance, sample_size):
    c = cutoff
    n = sample_size
    sigma = np.sqrt(variance)
    
    k = (c*variance)/(n*(m_1-m_0)) + (m_1+m_0)/2.0
    
    z_alpha = (k-m_0)/(sigma/np.sqrt(n))
    
    # Pr{z_score >= z_alpha}
    return 1.0 - st.norm(loc=0, scale=1).cdf(z_alpha)

For $\beta$ ...

$$ \beta = \text{Pr}_{f_1} \{\bar{x} \lt k\} = \text{Pr}_{f_1} \{\bar{x} - \mu_1 \lt k - \mu_1\} $$

$$ \beta = \text{Pr}_{f_1} \left\{\frac{\bar{x} - \mu_1}{\frac{\sigma}{\sqrt{n}}} \lt \frac{k - \mu_1}{\frac{\sigma}{\sqrt{n}}}\right\} $$

$$ \beta = \text{Pr}_{f_1} \left\{\text{z-score} \lt \frac{k - \mu_1}{\frac{\sigma}{\sqrt{n}}}\right\} \enspace \enspace \text{ where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

resulting in the python code below:

def beta_calculation(cutoff, m_0, m_1, variance, sample_size):
    c = cutoff
    n = sample_size
    sigma = np.sqrt(variance)
    
    k = (c*variance)/(n*(m_1-m_0)) + (m_1+m_0)/2.0
    
    z_beta = (k-m_1)/(sigma/np.sqrt(n))
    
    # Pr{z_score < z_beta}
    return st.norm(loc=0, scale=1).cdf(z_beta)

and the code ...

alphas_calculated = []
betas_calculated = []
for cutoff in cutoffs:
    alpha_ = alpha_calculation(cutoff, 0.0, 0.5, 1.0, sample_size)
    beta_ = beta_calculation(cutoff, 0.0, 0.5, 1.0, sample_size)
    
    alphas_calculated.append(alpha_)
    betas_calculated.append(beta_)

and the code ...

# Reproducing Figure 2.2 from calculation results.
plt.xlabel('$\\alpha$')
plt.ylabel('$\\beta$')
plt.xlim(-0.1, 1.05)
plt.ylim(-0.1, 1.05)
plt.axvline(x=0, color='b', linestyle='--')
plt.axvline(x=1, color='b', linestyle='--')
plt.axhline(y=0, color='b', linestyle='--')
plt.axhline(y=1, color='b', linestyle='--')
figure_2_2 = plt.plot(alphas_calculated, betas_calculated, 'ro', alphas_calculated, betas_calculated, 'k-')

to obtain a figure and values for $\alpha$ and $\beta$ very similar to my first simulation

enter image description here

And finally to compare the results between simulation and calculation side by side ...

df = pd.DataFrame({
    'cutoff': np.round(cutoffs, decimals=2), 
    'simulated alpha': np.round(alphas_simulated, decimals=2),
    'simulated beta': np.round(betas_simulated, decimals=2),
    'calculated alpha': np.round(alphas_calculated, decimals=2),
    'calculate beta': np.round(betas_calculated, decimals=2)
})
df

resulting in

enter image description here

This shows that the results of the simulation are very similar (if not the same) to those of the analytical approach.

In short, I still need help figuring out what might be wrong in my calculations. Thanks. :)

Community
  • 1
Francisco Fonseca
  • 131
  • 6
  • 3
    It seems to me that any question that requires readers to wade through 11 pages of computer code, statistical output, and algebra is unlikely to be read by anybody, much less answered cogently. If you are interested in pursuing this, as you seem to be from the time and attention you have spent on it, might I suggest that you identify the crux of the matter and see if you can explain it and ask your question within the space of one or at most two pages of material? – whuber Dec 26 '18 at 20:10
  • 1
    Hi @whuber, thank you for your suggestion! My intention was to post details (source code and explanations) to allow anyone to reproduce my results, but it seems that this strategy did not work very well as you correctly observed :). Thank you again. Then I edited the question to summarize my doubt at the beginning of the post. I hope this works. – Francisco Fonseca Dec 26 '18 at 21:48

1 Answers1

4

In the website of the book Computer Age Statistical Inference, there is a discussion session where Trevor Hastie and Brad Efron often reply to several questions. So, I posted this question there (as below) and received from Trevor Hastie the confirmation that there is an error in the book that will be fixed (in other words, my simulations and calculations - as implemented in Python in this question - are correct).

enter image description here

When Trevor Hastie replied that "In fact c=.75 for that plot" means that at the figure below (original Figure 2.2 from the book) the cutoff $c$ should be $c=0.75$ instead of $c=0.4$:

enter image description here

So, using my functions alpha_simulation(.), beta_simulation(.), alpha_calculation(.) and beta_calculation(.) (whose the full Python code is available in this question) I got $\alpha=0.10$ and $\beta=0.38$ for a cutoff $c=0.75$ as a confirmation that my code is correct.

alpha_simulated_c075 = alpha_simulation(0.75, f0_density, f1_density, sample_size, replicates)
beta_simulated_c075 = beta_simulation(0.75, f0_density, f1_density, sample_size, replicates)

alpha_calculated_c075 = alpha_calculation(0.75, 0.0, 0.5, 1.0, sample_size)
beta_calculated_c075 = beta_calculation(0.75, 0.0, 0.5, 1.0, sample_size)

print("Simulated: c=0.75, alpha={0:.2f}, beta={1:.2f}".format(alpha_simulated_c075, beta_simulated_c075))
print("Calculated: c=0.75, alpha={0:.2f}, beta={1:.2f}".format(alpha_calculated_c075, beta_calculated_c075))

enter image description here

Finally, when Trevor Hastie replied that "... resulting in a threshold for x of .4" it means that $k=0.4$ in the equation below (see section B from this question):

$$ \bar{x} \ge k \text{, where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

resulting in

$$ t_c(x) = \left\{ \begin{array}{ll} 1\enspace\text{if } \bar{x} \ge k\\ 0\enspace\text{if } \bar{x} \lt k.\end{array} \right. \enspace \enspace \text{, where } k = \frac{c\sigma^2}{n\left(\mu_1-\mu_0\right)} + \frac{\left(\mu_1+\mu_0\right)}{2} $$

So, in Python we can get $k=0.4$ for a cutoff $c=0.75$ as below:

n = 10
m_0 = 0.0
m_1 = 0.5
variance = 1.0
c = 0.75

k = (c*variance)/(n*(m_1-m_0)) + (m_1+m_0)/2.0
threshold_for_x = k

print("threshold for x (when cutoff c=0.75) = {0:.1f}".format(threshold_for_x))

enter image description here

Francisco Fonseca
  • 131
  • 6