I am dealing with compositional data, in a high dimension.
Each sample I have behaves like:
$$ {S}^D=\left\{\mathbf{x}=[x_1,x_2,\dots,x_D]\in\mathbb{R}^D \,\left|\, x_i>0,i=1,2,\dots,D; \sum_{i=1}^D x_i=1 \right. \right\} $$
In order to embed the high-dimensional data for visualization into a low-dimensional space of two or three dimensions, I use different methods with respect to $Euclidean$ distances, for example t-SNE
In order to maintain distances with respect to Aitchison geometry I use the Central Logratio Transformation (CLR) before applying the dimensional reduction:
$$ \operatorname{clr}(x) = \left[ \log \frac{x_1}{g(x)} \cdots \log \frac{x_{D-1}}{g(x)} \right] $$
where $ g(x) $ is the geometric mean of the sample.
$ clr $ has shown significant improvement in visualizing the data, and preserving its natural patterns (measured by tightness of pre-known clusters in the data).
However, I get very similar improvements by simply applying $Log$ transformation to the data:
$$ \operatorname{log}(x) = \left[ \log x_1 \cdots \log x_{D-1} \right] $$
$Log$ captures a lot of the essense of the $clr$, but I want to prove that $clr$ is the right way to go when trying to preserve $Euclidean$ distances in the data.
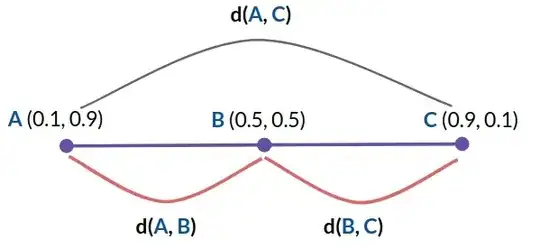
To try that, I have tested the 2D case of two points along the Aitchison simplex:
$$ A = \left[0.1, 0.9 \right], C = \left[0.9, 0.1 \right] $$
In order to move from point $A$ to $C$ along the simplex I have to traverse via point $ B = \left[0.5, 0.5 \right] $:
In the $clr$ space the Euclidean distances are preserved in a way that:
$$ d(clr(A), clr(B)) + d(clr(B), clr(C)) = d(clr(A), clr(C))$$
However in $Log$ space we get the following behavior:
$$ d(log(A), log(B)) + d(log(B), log(C)) > d(log(A), log(C))$$
Which indicates the $Log$ can distort the Euclidean distances in a way that might create problems.
Is there a better way to prove that $clr$ or similar transformation that maintain Aitchison geometry are superior in such cases?