4

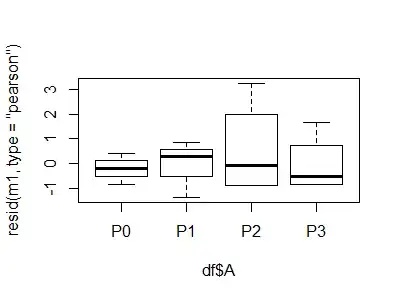
I fitted a beta regression on some proportion data using the betareg() function from the betareg package. The proportion was scaled using the ad-hoc scaling procedure recommended in the betareg vignette (Section 2; 1st paragraph):

vignette("betareg", package = "betareg")

My sample size is $n = 4$, which I know is very limited. After plotting the residuals I saw evidence of heteroskedasticity and decided to include the precision parameter $\phi$ into the model. After that the residuals looked fine and I wanted to get the estimated marginal means of the model using the emmeans() function from the emmeans package. There I saw that one of the lower confidence limits extends into the negative (only for the model that includes $\phi$ though).

My question is, is that possible given the beta distribution?

Below a reproducible example:

df <- structure(list(A = structure(c(1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 
3L, 3L, 3L, 3L, 4L, 4L, 4L, 4L), .Label = c("P0", "P1", "P2", 
"P3"), class = "factor"), PROP = c(0.2, 0.1, 0.2, 0.3, 0.1, 0.4, 
0.4, 0.5, 0.5, 0, 0, 0.2, 0.2, 0.5, 0.1, 0.1), PROP_SCALED = c(0.2046875, 
0.10625, 0.2046875, 0.303125, 0.10625, 0.4015625, 0.4015625, 
0.5, 0.5, 0.0078125, 0.0078125, 0.2046875, 0.2046875, 0.5, 0.10625, 
0.10625)), class = "data.frame", row.names = c(NA, -16L))

require(betareg)
require(emmeans)

m1 <- betareg(PROP_SCALED ~ A, data = df)
# summary(m1)
plot(resid(m1, type = "pearson") ~ df$A)

enter image description here

m2 <- betareg(PROP_SCALED ~ A | A, data = df)
# summary(m2)
plot(resid(m2, type = "pearson") ~ df$A)

enter image description here

Note the negative LCL for P2:

emmeans(m2, "A")
#A     emmean         SE  df   asymp.LCL asymp.UCL
#P0 0.2044328 0.03557230 Inf  0.13471239 0.2741532
#P1 0.3453680 0.07860826 Inf  0.19129859 0.4994373
#P2 0.1722369 0.09659308 Inf -0.01708209 0.3615558
#P3 0.2335368 0.07133364 Inf  0.09372545 0.3733482

#Confidence level used: 0.95

For comparison the emmeans for the model without $\phi$:

emmeans(m1, "A")
#A     emmean         SE  df  asymp.LCL asymp.UCL
#P0 0.2386583 0.07473188 Inf 0.09218648 0.3851300
#P1 0.3506016 0.08650745 Inf 0.18105014 0.5201531
#P2 0.1157728 0.04966404 Inf 0.01843309 0.2131125
#P3 0.2407182 0.07502464 Inf 0.09367255 0.3877638

#Confidence level used: 0.95
Scortchi - Reinstate Monica
  • 27,560
  • 8
  • 81
  • 248
Stefan
  • 4,977
  • 1
  • 18
  • 38
  • 3
    I believe most of the explanation will ultimately rest on your efforts to use methods that are hard to justify for such a small dataset. Certainly anything with `asymp.` in its name ("asymptotic") is unlikely to be accurate. Also, with just four samples per group it's almost impossible to detect *any* amount of heteroscedasticity, suggesting you haven't enough information to support using the additional parameter $\phi.$ We shouldn't be surprised at unrealistic interval endpoints, then, and perhaps even should welcome them as indicating the method isn't over-confident in its results. – whuber Dec 11 '18 at 22:43
  • 1
    Thanks for your comment and insight @whuber . The lack of samples is clearly a problem I know. So in a way it is probably the best to simply forgo any inferential statistics and simply describe and visualize the data descriptively since it won't be possible to do any meaningful model validations anyway. – Stefan Dec 11 '18 at 22:54

0 Answers0