6

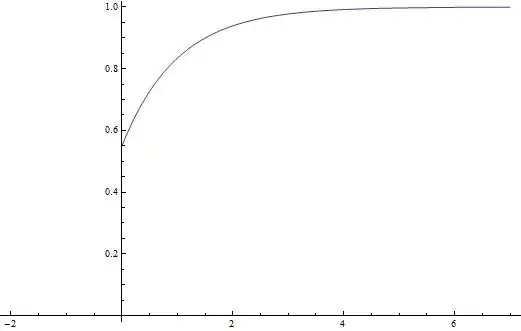
Let $X$ be an exponential random variable $f(x) = c e^{-c x} \text{ if }x > 0; 0 \text{ otherwise.}$ Let $Z$ be a Bernoulli RV with $Pr(Z=1)=0.45$ and $Pr(Z=0)=0.55$.

$X$ and $Z$ are independent.

Let $Y$ be the product of $X$ and $Z$: $Y=XZ$. What's the distribution of $Y$?

Here's my attempt:

$Pr(Y\leqslant y)=Pr(XZ\leqslant y)=Pr(XZ\leqslant y \cap Z=1)+Pr(XZ\leqslant y \cap Z=0)$

Due to independence, the above equation becomes

$$ \begin{align} &Pr(XZ\leqslant y)Pr(Z=1)+ Pr(XZ\leqslant y)Pr(Z=0)\\ =&Pr(X\leqslant y)Pr(Z=1)+ Pr(0\leqslant y)Pr(Z=0)\\ =&0.45Pr(X\leqslant y)+0.55Pr(y\geqslant 0) \end{align} $$

Plug in $Pr(X\leqslant y)=F_X(y)$ and $Pr(y\geqslant 0)=1$:

$Pr(Y\leqslant y)=0.45(1-e^{-cy})+0.55=1-0.45e^{-cy}$

But this can't be right: it's not a valid cdf. What did I do wrong here? Thanks in advance!

Edit: it is a correct cdf. I had a brain freeze for a moment.

tcollar
  • 71
  • 3

2 Answers2

6

I don't know why you call this an invalid CDF.

You have a mixed random variable $Y$:

$$Y=XZ=\begin{cases}0&,\text{ if }Z=0\\X&,\text{ if }Z=1\end{cases}$$

So the distribution function of $Y$ must be

\begin{align} P(Y\le y)&=P(XZ\le y) \\\\&=P(XZ\le y\mid Z=0)P(Z=0)+P(XZ\le y\mid Z=1)P(Z=1) \\\\&=\begin{cases}P(Z=0)+P(X\le y)P(Z=1)&,\text{ if }y\ge0 \\0&,\text{ if }y<0\end{cases} \\\\&=\begin{cases}0.55+0.45(1-e^{-cy})&,\text{ if }y\ge0\\ 0&,\text{ if }y<0\end{cases} \end{align}

That is,

$$F(y)=P(Y\le y)=\begin{cases}1-0.45e^{-cy}&,\text{ if }y\ge0\\ 0&,\text{ if }y<0\end{cases}$$

Taking $c=1$, the plot of $F(y)$ looks like

enter image description here

If you check the conditions of a valid CDF, you will see that $F$ satisfies all those conditions.

StubbornAtom
  • 8,662
  • 1
  • 21
  • 67
  • 1
    I made a mistake. I thought when $y$ approaches $\infty$, $e^{-cy}$ approaches 1, so $F(y)$ $\rightarrow$ 0.55. Actually, when $y$ approaches $\infty$, $e^{-cy}$ approaches 0. $F(y)$ is a valid cdf. – tcollar Dec 12 '18 at 02:10
0

The first three central moments of $Y$ are as follows:

The expectation of $Y$ can be written as: $$\displaystyle \mu_{{1}}\, = \, E(Y) \, = \, 0 \, (1-p) \, + \, \int_{0}^{\infty }\!\, p \, y \, c \,{{\rm e}^{- c \,y}}\,{\rm d}y \,= \, \frac {p}{ c }$$ The variance of $Y$ can be writt en as: $$\displaystyle \mu_{{2}}\, = \, Var(Y) \, = \, (1-p) \, \left(0-\frac{p}{ c }\right) ^2 +\int_{0}^{\infty }\!p \, \left( y-{\frac {p}{ c }} \right) ^{2} c \,{{\rm e}^{- c \,y}}\,{\rm d}y \, = \,-{\frac {p \left( p-2 \right) }{{ c }^{2}}}$$ The third central moment can be written as: $$\displaystyle \mu_{{3}}\, = \, (1-p) \, \left(0-\frac{p}{ c }\right) ^3 +\int_{0}^{\infty }\!p \, \left( y-{\frac {p}{ c }} \right) ^{3} c \,{{\rm e}^{- c \,y}}\,{\rm d}y \, = \,2\,{\frac {p \left( {p}^{2}-3\,p+3 \right) }{{ c }^{3}}}$$

with $p = Pr(Z=1)$ and $(1-p) = Pr(Z=0)$.

Ad van der Ven
  • 127
  • 5