If the joint probability is the intersection of 2 events, then shouldn't the joint probability of 2 independent events be zero since they don't intersect at all? I'm confused.
-
19The probability that I watch on a given day TV is 1/2. The probability that it rains on a given day is 1/2. These are independent events. What is the probability of me watching TV on a rainy day? – user1936752 Dec 07 '18 at 18:18
-
5@user1936752 Strictly speaking, your example events are *not* independent for most people (e.g., they might be more willing to spend time outdoors when it does not rain) – Hagen von Eitzen Dec 09 '18 at 12:41
-
@HagenvonEitzen OK, good point. Change *rainy day* to *eat chocolate*. – Rui Barradas Dec 10 '18 at 10:44
-
2@Gaston: Don't confuse "independent" with "mutually exclusive". _Independent_ events are completely unrelated to each other, whereas _mutually exclusive_ events are **inherently** related. For example, suppose I flip two coins: whether I get heads on Coin 1 is unaffected by the result of Coin 2, but it's inherently connected to whether I get tails on Coin 1! =) – jdmc Dec 10 '18 at 17:45
-
1This video [here](https://www.youtube.com/watch?v=pV3nZAsJxl0&list=PLvxOuBpazmsOGOursPoofaHyz_1NpxbhA&index=5) and [this](https://www.youtube.com/watch?v=UOfsad9WWwk&index=6&list=PLvxOuBpazmsOGOursPoofaHyz_1NpxbhA) other one will be helpful in understanding these concepts. – Learn_and_Share Dec 11 '18 at 22:59
3 Answers
There is a difference between
- independent events: $\mathbb P(A \cap B) =\mathbb P(A)\,\mathbb P(B)$, i.e. $\mathbb P(A \mid B)= \mathbb P(A)$ so knowing one happened gives no information about whether the other happened
- mutually disjoint events: $\mathbb P(A \cap B) = 0$, i.e. $\mathbb P(A \mid B)= 0$ so knowing one happened means the other did not happen
You asked for a picture. This might help:
- 103
- 2
- 30,848
- 1
- 63
- 107
-
is it possible to illustrate this with shapes/drawings? I'd be very grateful if you can point me to any drawings. Sorry I understand better with drawings/geometry – gaston Dec 07 '18 at 09:00
-
-
7Is there a reason you wrote "almost" in the second bullet point? Is that one of those "possible with probability zero" things? I would think it is by definition impossible (such as the probability of heads and the probability of tails), then why write "almost certainly" rather than "certainly"? I suppose this is the probabilistic interpretation. – gerrit Dec 07 '18 at 10:51
-
1@gerrit because an event *can* occur, even if it's probability is zero. For example, the probability of not winning and not loosing when throwing a fair coin is zero, *but it can land on its side in a crack of the floor*: P{Heads}=P{Tails}=0.5, and P{Not Heads Or Tails}=0, and yet "No Heads or Tails" can happen – Barranka Dec 07 '18 at 12:26
-
3@Barranka I get that, but that doesn't look like what is drawn in the picture on right. The joint probability of a uniformly drawn random number in [0, 1] being both smaller than 0.4 and larger than 0.6 is not only zero, it is also completely impossible. Isn't that what the wide band in the right figure illustrates? Or am I misreading the figure? – gerrit Dec 07 '18 at 13:13
-
2@Barranka I could throw the coin so fast that it escapes earth's gravitational pull. I would venture P(HEADS)=0.499..., P(TAILS)=0.499..., 0 – emory Dec 07 '18 at 13:24
-
4I'm no expert, but even after your last comment I agree with @gerrit: *Heads* and *Tails* are disjoint. It's possible to get *Not heads and not tails*, but it's impossible to get *heads and tails*. Thus knowing *heads* happened means that *tails* **could not possibly** have happened - no "almost" about it. I could be wrong on my terminology, but if so please explain patiently as I'm not the only one missing it – Chris H Dec 07 '18 at 13:53
-
Maybe it's clearer to say "An event with zero probability *is* posible, although it's occurrence is so unlikely that it's measure of occurrence is zero". In the example of a coin, both results are mutually disjoint (they cannot happen at the same time), but the "Empty" result (no result), although its probability is zero, can happen. The "almost" part in the answer deals with such occurrences, I think. – Barranka Dec 07 '18 at 15:31
-
1I think the right graph would be much clearer if A label is below the B label. Then it is much more clear that they are disjoint – gota Dec 07 '18 at 15:42
-
@gerrit "[Almost certainly](https://en.wikipedia.org/wiki/Almost_surely)" is a term of art in probability. In certain situations (particularly with infinite outcome sets) you can have P(X)=0 and still see an event. E.g. Pick a random natural number from the full set of natural numbers. What's the probability that it's even? What's the probability that it's prime? What's the probability that it's prime *and* even? -- If you picked an prime number, would you say it's impossible that it's even? – R.M. Dec 07 '18 at 18:03
-
1@R.M. I'm aware of that, as I stated in [my comment replying to Barranka](https://stats.stackexchange.com/questions/380789/shouldnt-the-joint-probability-of-2-independent-events-be-equal-to-zero/380791?noredirect=1#comment715867_380791), but that doesn't apply to the joint probability of the outcomes x<0.5 and x>0.5, or does it? When two outcomes are mutually disjoint, does that not mean that it's *by definition* absolutely certain (not almost certain), that they are not both true? – gerrit Dec 07 '18 at 18:33
-
2@Braanka Your coin example is a poor one, as presumably landing on a side has non-zero probability, and if you say that it has zero probability, well, now you're pretty much just begging the question. – Acccumulation Dec 07 '18 at 19:45
-
2The only explanation for saying that something has p=0 but could happen that I can think of is if one is distinguishing between a set that has measure zero versus a set that is empty. In a normal distribution, the probability of getting a value *exactly* equal the mean is zero (it's a measure zero set), but that's true of every particular value, and obviously when you take a sample, you get *some* value (although, practically, one doesn't measure to infinite accuracy, and given any measured value, the set of actual values that would be measured as having that value has non-zero measure). – Acccumulation Dec 07 '18 at 19:46
-
Another example is flipping a coin an infinite number of times. Any particular sequence of heads and tails has probability zero of happening, and yet *some* sequence will come up (if one could actually flip a coin an infinite number of times, that is). – Acccumulation Dec 07 '18 at 19:46
What I understood from your question, is that you might have confused independent events with disjoint events.
disjoint events: Two events are called disjoint or mutually exclusive if they cannot both happen. For instance, if we roll a die, the outcomes 1 and 2 are disjoint since they cannot both occur. On the other hand, the outcomes 1 and “rolling an odd number” are not disjoint since both occur if the outcome of the roll is a 1. The intersect of such events is always 0.
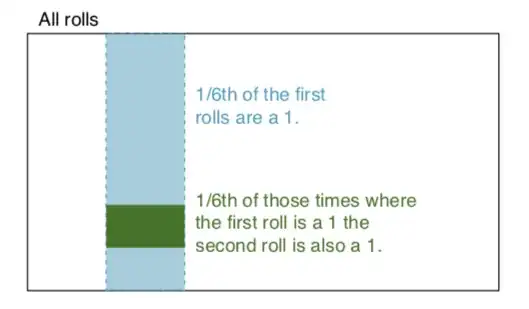
independent events: Two events are independent if knowing the outcome of one provides no useful information about the outcome of the other. For instance, when we roll two dice, the outcome of each is an independent event – knowing the outcome of one roll does not help determining the outcome of the other. Let's build on that example: We roll two dice, a red and a blue. The probability of getting a 1 on the red is given by P(red = 1) = 1/6, and the probability of getting a 1 on the white is given by P(white = 1) = 1/6. It is possible to get their intersect (i.e. both get 1) simply by multiplying them, since they are independent. P(red = 1) x P(white = 1) = 1/6 x 1/6 = 1/36 != 0. In simple words 1/6 of the time the red die is a 1, and 1/6 of those times the white die is 1. To illustrate:
- 131
- 5
The confusion of the OP lies on the notions of disjoint events and independent events.
One simple and intuitive description of independence is:
A and B are independent if knowing that A happened gives you no information about whether or not B happened.
Or in other words,
A and B are independent if knowing that A happened does not change the probability that B happened.
If A and B are disjoint then knowing that A happened is a game changer! Now you would be certain that B did not happen! And so they are not independent.
The only way independence and "disjointedness" in this example are the same is when B is the empty set (which has probability 0). In this case A happening does not inform anything on B
No pictures but at least some intuition
- 183
- 7