I am writing a follow up question regarding a closed Cross Validated question previosuly. The original question can be found here
To give a breif overview, I am using the following code to produce a decision tree.
data(agaricus.train, package='xgboost')
bst <- xgboost(data = agaricus.train$data, label = agaricus.train$label, max_depth = 3,
eta = 1, nthread = 2, nrounds = 2,objective = "binary:logistic")
# plot all the trees
xgb.plot.tree(model = bst)
# plot only the first tree and display the node ID:
xgb.plot.tree(model = bst, trees = 0, show_node_id = TRUE)
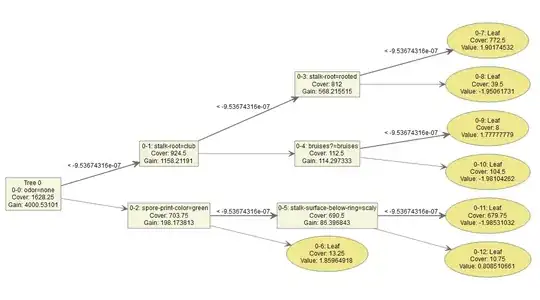
The output gives the following tree:
I was referred to the following answer from a previous CV question here. It answered some questions but I still have one or two additional doubts regarding my intuition.
The answer states
'Each node in the tree has an associated "weight."'
So using the tree example above each decision node will have a "weight" which is not displayed. That is node 0-0 will have a weight, node 0-2 will have another weight, node 0-5 will have an additional weight. Then the terminal node is a summation over all the "weights" preceding it, i.e. nodes 0-0, 0-2 and 0-5 and depending on which side of the split we end up we obtain a value (or final weight) of 0.8085 or -1.985. Is this correct?
XGBoost then constructs another tree (tree 1) where the features are in different positions in the tree and the split numbers are also different. Then the observations will fall into different terminal nodes and because the features are in different positions in the tree the summation of all the "weights" in the terminal node will be different. So an observation which fell into terminal node 0-12 in tree 0 may now fall into terminal node 1-8 in tree 1. With two terminal scores/weights. This will go on for say 100 trees in our model, so each observation will have 100 terminal weight-scores, these weights/scores are then summed up and we obtain a log-odds score for each observation which can be converted to a predicted probability. - Is this correct?
EDIT:
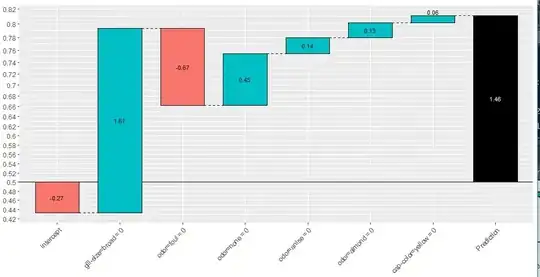
If my above intuition has been misplaced and the quote "Each Terminal node in the tree has an associated "weight" is now correct. Then regarding the "XGBoost explainer" package how are the individual features "log-odds" scores calculated. The below code gives me the following xgboostExplainer output.
Each feature in the dataset obtains a log-odds score for a particular observation which I plot the waterfall plot for observation x. My understanding is that each "value" inside the blue/red boxes are log-odds scores for a given feature (each score will be different depending on the observation we plot).
So what I know is;
We have a "value" / log-odds contribution at the terminal node of each tree (given by figure 1) - which is determined from a specific path an observation takes through the tree.
We also have individual log-odds scores for each feature (given by the blue/red boxes in the waterfall plots in figure 2).
Where is my misunderstanding coming from? - if we only obtain terminal leaf node weights/scores/log-odds values from a given path an observation takes then where are the individual feature log-odds scores coming from? - since my understanding is the log-odds scores are coming from a combination of feature splits determined at the final terminal leaf node.
library(xgboost)
library(xgboostExplainer)
set.seed(123)
data(agaricus.train, package='xgboost')
X = as.matrix(agaricus.train$data)
y = agaricus.train$label
train_idx = 1:5000
train.data = X[train_idx,]
test.data = X[-train_idx,]
xgb.train.data <- xgb.DMatrix(train.data, label = y[train_idx])
xgb.test.data <- xgb.DMatrix(test.data)
param <- list(objective = "binary:logistic")
xgb.model <- xgboost(param =param, data = xgb.train.data, nrounds=3)
col_names = colnames(X)
pred.train = predict(xgb.model,X)
nodes.train = predict(xgb.model,X,predleaf =TRUE)
trees = xgb.model.dt.tree(col_names, model = xgb.model)
#### The XGBoost Explainer
explainer = buildExplainer(xgb.model,xgb.train.data, type="binary", base_score = 0.5, trees = NULL)
pred.breakdown = explainPredictions(xgb.model, explainer, xgb.test.data)
showWaterfall(xgb.model, explainer, xgb.test.data, test.data, 2, type = "binary")
showWaterfall(xgb.model, explainer, xgb.test.data, test.data, 8, type = "binary")