I had frequently seen the definition for a "rigorous" spatial isotropic semivariogram being defined as:
$$ \gamma(h) = K(0) - K(h) $$
Where $K$ is a positive definite covariance matrix. If the nugget $\sigma$ is applied to the covariance function $K$, then it seems to me that it would always be that $\gamma(0) = 0$, but that $\gamma(0+\delta)>\sigma$ for all distances greater than zero.
However, often in practice a linear function is used to determine $\gamma$:
$$ \gamma(h) = \sigma + \frac{h}{\beta} $$
Should I really define the nugget in terms of the covariance matrix, or should I make it a separate term:
$$ \gamma(h) = \sigma + K(0) - K(h) $$
Am I making a mountain out of mole hill here? Are there any reasons to prefer one form or the other?
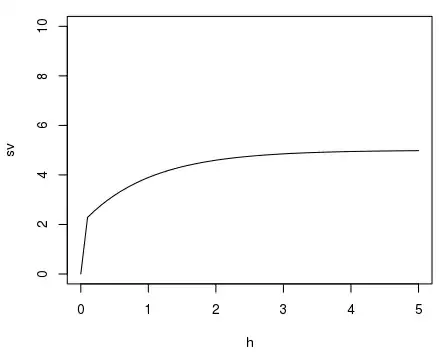
To visualize, is it more "correct" to pick one form over the other:
Based on the idea of nugget as allowing a non-zero offset at zero, I could see the former should be preferred: but this seems to imply that the nugget is no really part of the assumed covariance matrix.