I am trying to predict a time-series data set, using python. I have a timestamp and number of calls in a network for this particular timestamp. I have to predict number of calls in the future. Currently, I have 90 days of data and for every 20 minutes in a day i have an entry with number of calls.
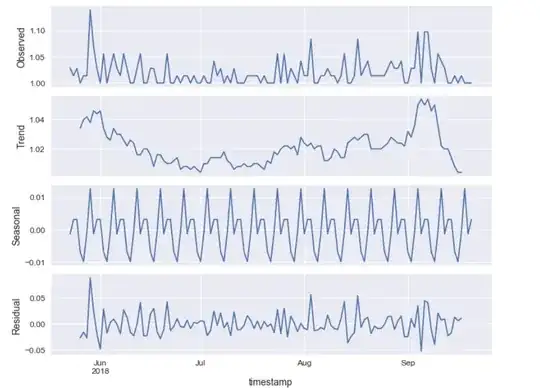
I resample the data so i plot the mean of the data for every 3 days and i get the following results:

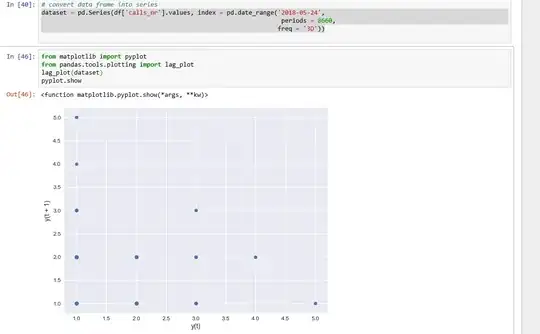
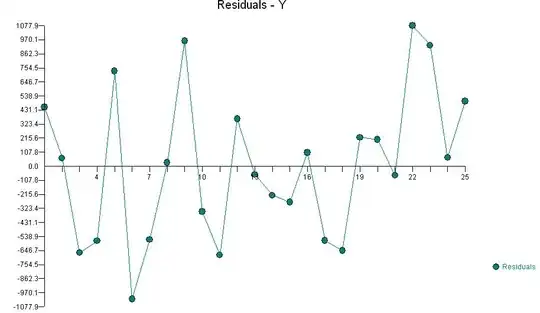
I am not sure the trend graph is saying much. The data is going up and down so no obvious trend. However, there is seasonality. After plotting this, I checked for autocorrelation and this is where the weirdness is happening I convert the created DataFrame to series and then plot it. This results in something weird, which shows just random values and no correlation
I do not know, if i am doing something wrong with my data, but if i have no autocorrelation and no stationarity, should i use Time Series analysis at all? And in general can I make any predictions on this data, maybe with linear regression? I am new to data science and i am doing this for my bachelor project, so i really need help. I have read a lot on the internet and maybe at this point i am pretty confused. Any help will be appreciated!
Regards
P.S
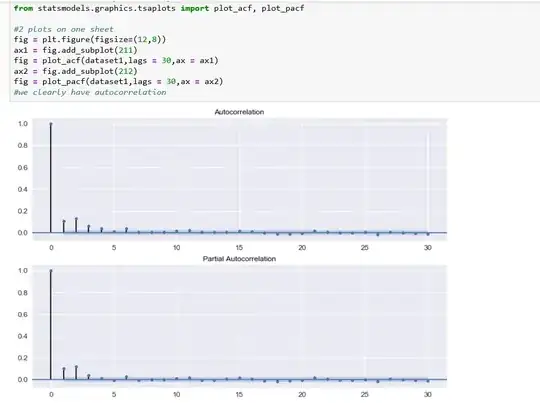
Here are some screen shots of acf and pacf plots with statsmodel library
First screenshot represents the data resampled to 3 days mean:
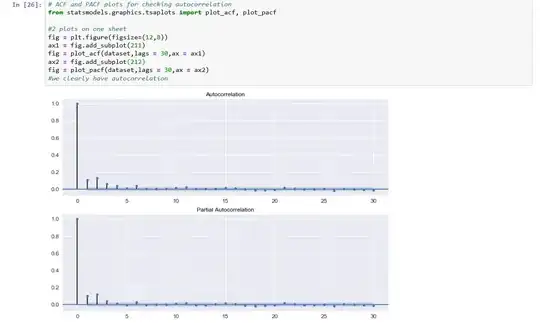
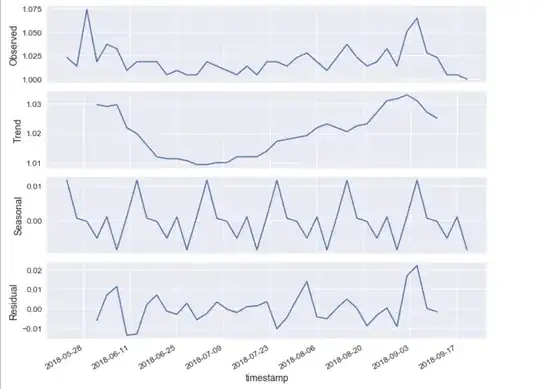
The acf and pacf for data resample to 1 day seems the same:
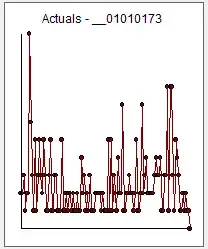
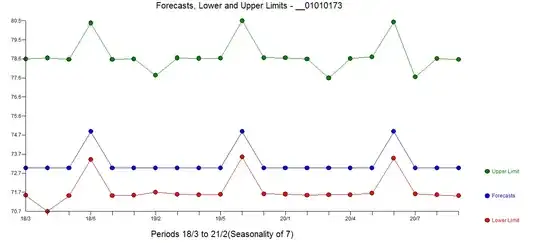
Here are the other plots as well for data resampled to 1 day