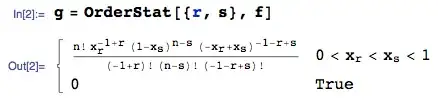4

I am trying to fit an ARIMA model to the following data minus the last 12 datapoints: http://users.stat.umn.edu/~kb/classes/5932/data/beer.txt

The first thing I did was take the log-difference to get a stationary process:

beer_ts <- bshort %>%pull(Amount) %>%ts(.,frequency=1)
beer_log <- log(beer_ts)
beer_adj <- diff(beer_log, differences=1)

. .

Both the ADF & KPSS tests indicates that beer_adj is indeed stationary, which matches my visual inspection: enter image description here . .

Fitting a model yields the following:

beer_arima <- auto.arima(beer_adj, seasonal=FALSE, stepwise=FALSE, approximation=FALSE)
summary(beer_arima)

Series: beer_adj 
ARIMA(4,0,1) with non-zero mean 

Coefficients:
         ar1     ar2     ar3      ar4      ma1    mean
      0.4655  0.0537  0.0512  -0.3486  -0.9360  0.0017
s.e.  0.0470  0.0517  0.0516   0.0469   0.0126  0.0005

sigma^2 estimated as 0.01282:  log likelihood=312.39
AIC=-610.77   AICc=-610.5   BIC=-582.68

Training set error measures:
                        ME      RMSE        MAE      MPE     MAPE     MASE        ACF1
Training set -0.0004487926 0.1124111 0.08945575 134.5103 234.3433 0.529803 -0.06818126

. .

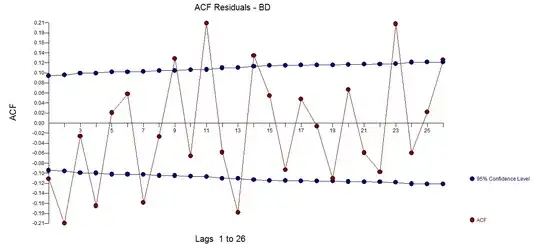
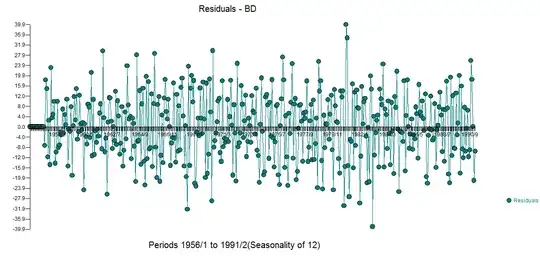
When inspecting the residuals, however, they seem to be serially autocorrelated at lag 12: enter image description here

I am unsure how I am supposed to interpret this last plot - at this stage I would have expected white noise residuals. I am new to time series analysis, but it seems to me that I am missing some fundamental step in my modelling here. Any pointers would be greatly appreciated!

Student_514
  • 43
  • 5

3 Answers3

8

You are looking at data for monthly beer production. It has seasonality that you must account for and it is this seasonality that you are noticing in your ACF plot. Note that you have 2 strands of seasonality - every 12 months (in the plot note the ACF being particularly high at 12 months and 24 months) and every 6 months (in the plot note the ACF being high at 6 months and 18 months).

As the next steps: - (1) Try adding lag12 into your model to account for the seasonality every 12 months, the strongest one you observe in the ACF plot - (2) If after step (1), you still have serial correlation, add both lag12 and lag6 into you model; this should take care of it

ColorStatistics
  • 2,699
  • 1
  • 10
  • 26
  • 1
    Every 6*k months seasonality where k is odd actually is 12-month seasonality, just with a phase shift from the original 12-month seasonality. – Richard Hardy Dec 01 '18 at 10:30
  • Good point, Richard. As is, I believe my answer is inconsistent because lag6 accounts for 6 month seasonality, while 6*k (where k is odd), refers, as you said, to a 12-month seasonality. After we've removed the seasonality at 12 months by introducing lag12 in the equation, we're still left with seasonality at 6 months, but, as I understand it, more so at those 6*k (where k is odd) months because lag12 would have already accounted for some of the seasonality at 6*k (where k is even). I think replacing "every 6*k (where k is odd)" with "every 6 months" should fix it. Let me know your thoughts. – ColorStatistics Dec 01 '18 at 11:49
  • 2
    There are two remedies for "seasonal dependency" 1) autoregressive and 2)seasonal pulses . Try adding three seasonal pulses ...one for january , a second for june and a third for october . – IrishStat Dec 01 '18 at 12:14
  • Thank you, IrishStat. Makes sense. I guess you'd call my proposed remedy "autoregressive". By "seasonal pulses ... one for january, a second for june and a third for october" are you referring to dummy variables, one for jan, another for june, and one for oct? I understand you arrived at the idea of adding seasonal pulses for january and october based on analysis supplementary to that provided in the question. The ACF plot provided in the question, as I read it, doesn't indicate anything about January and not much evidence about October (assuming jan start of data - autocorrelation at 10, 22). – ColorStatistics Dec 01 '18 at 13:15
  • yes add three series ... all 0/1 . The ACF is a portmanteau (global) statistic and doesn't speak to the effect of individual months . Yes ARIMA is both autoregressive and purely endogenous. Adding user specified variables/series adds exogenous structure irrespective of whether they were known a priori or discovered. via Intervention Detection. Note well that your series (error series) also has many pulses unusual one-time values and if left untreated you will get a bloated error variance leading to a downwards bias on all coefficients. I will add another comment. – IrishStat Dec 01 '18 at 17:21
  • 1
    The seasonal pulse for jan(1) starts at period 73 ... the seasonal pulse for oct (10) starts at period 31 and the seasonal pulse for june(6) starts at period 78. Values before these periods would be 0 for three variables/series. It is very important especially in a classroomlearning context to teach what is right and what should be done .. even if it "complicates" as teaching insufficient methodology is never a good strategy. – IrishStat Dec 01 '18 at 17:28
6

If I am not mistaken, the observations in this beer time series were collected 12 times a year for each year represented in the data, so the frequency of the time series is 12.

As explained at https://www.statmethods.net/advstats/timeseries.html, for instance, frequency is the number of observations per unit time. This means that frequency = 1 for data collected once a year, frequency = 4 for data collected 4 times a year (i.e., quarterly data) and frequency = 12 for data collected 12 times a year (i.e., monthly data). Not sure why you would use frequency = 1 instead of frequency = 12 for this time series?

For time series data where frequency = 4 or 12, you should be concerned about the possibility of seasonality (see https://anomaly.io/seasonal-trend-decomposition-in-r/).

If seasonality is present, you should incorporate this into your time series modelling and forecasting, in which case you would use seasonal = TRUE in your auto.arima() function call.

Before you construct the ACF and PACF plots, you can diagnose the presence of seasonality of a quarterly or monthly time series using functions such as ggseasonplot() and ggsubseriesplot() in the forecast package in R, as seen here: https://otexts.org/fpp2/seasonal-plots.html.

Isabella Ghement
  • 18,164
  • 2
  • 22
  • 46
  • 1
    This is the only correct answer. Specifying `frequency=12` in the `ts()` call yields a seasonal time series, and `auto.arima()` then fits a nice seasonal model, ARIMA(4,1,2)(0,1,2)[12]. There are still a few "significant" peaks in the (P)ACF plots for the residuals, which I personally would put down to a long series and not worry unduly about. – Stephan Kolassa Dec 01 '18 at 13:31
  • Thank you so much, Stephan! The asker of the question can examine model diagnostics for the model suggested by auto.arima() and also perform time series cross validation to assess the accuracy of forecasts at each specific forecast horizon considered. I agree with you that there is no need to get overly complicated when modelling this time series, especially in a learning context. – Isabella Ghement Dec 01 '18 at 13:39
  • 1
    Thank you both for your answers, that makes complete sense. With that said, @StephanKolassa, simply setting `frequency=12` does not then give me the same auto.arima model you are getting. What I get is ARIMA(1,0,3)(1,0,0)[12] for the log-differenced series. This is with: `auto.arima(beer_adj, seasonal=TRUE, stepwise=FALSE, approximation=FALSE)`. I can model it manually at this stage but I was curious to know if you had to modify anything else for the auto.arima to yield the desired result. Thanks! – Student_514 Dec 02 '18 at 14:59
  • 2
    Interesting. My code is `beer_ts – Stephan Kolassa Dec 02 '18 at 15:18
  • 1
    @Student_514: It sounds like Stephan is applying auto.arima() to the original beer_ts series while you are applying it to beer_adj (i.e., the log-differenced series). The auto.arima() function is 'smart enough' to know what Box-Cox transformation and differencing to apply to the original series, so it's sufficient to supply the original series to auto.arima(). – Isabella Ghement Dec 02 '18 at 16:11
1

You say "log-difference to get a stationary process" . One doesn't take logs to make the series stationary When (and why) should you take the log of a distribution (of numbers)? , one takes logs when the expected value of a model is proportional to the error variance. Note that this is not the variance of the original series ..although some textbooks and statisticians make this mistake.

It is true that there appears to be "larger variablilty" at higher levels BUT it is more true that the error variance of a useful model changes deterministically at two points in time . Following http://docplayer.net/12080848-Outliers-level-shifts-and-variance-changes-in-time-series.html we find that enter image description here

The final useful model accounting for a needed difference and a needed Weighted Estimation (via the identified break points in error ) and ARMA structure and adjustments made for anomalous data points is here .enter image description here

Also note that while seasonal arima structure can be useful (as in this case ) possibilities exist for certain months of the year to have assignable cause i.e. fixed effects. This is true in this case as months (1,6 and 10) have significant deterministic impacts ... Jan & June are higher while October is significantly lower.

The residual acf suggests sufficiency ( note that with 422 values the standard deviation of the acf roughly is 1/sqrt(422) yielding many false positives enter image description here . The plot of the residuals suggest sufficiency enter image description here . The forecast graph for the next 12 values is here enter image description here

IrishStat
  • 27,906
  • 5
  • 29
  • 55