Measure of smoothness

Question

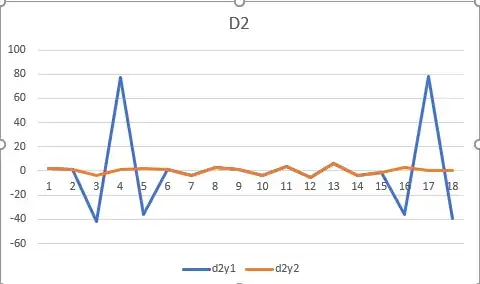
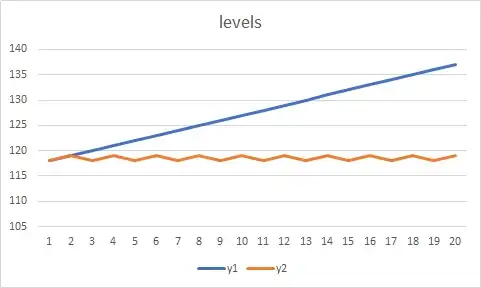
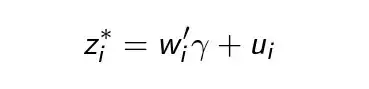I have an image that has artefacts which I am using a specific process to remove. I want to show that the new image is improved by that process. To compare the two images I am using data from a specific row of the image.

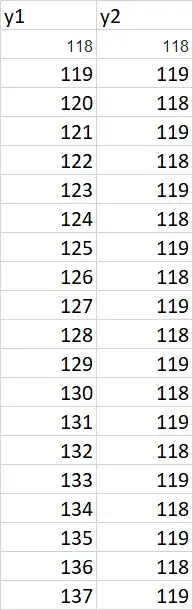
This would be the data (intensity of one specific row) before the change:

y1=[118 117 118 120 80 117 118 120 118 119 121 119 121 118 121 120 118 80 120 121]

and the data after the process:

y2=[118 117 118 120 118 117 118 120 118 119 121 119 121 118 121 120 118 119 120 121]

The above data are not all the data (there are tens of thousands of data points, this is just an example). I know that there are ways to show that the two datasets are different but what I want to show is that the second dataset is now more smooth, therefore the new image has been improved.

Is anyone aware of such a metric?

Answer 1

The conventional smoothness measures are based on derivatives, and are sometimes called "roughness." For instance, in smoothing splines there's a roughness penalty, which you minimize to get the smooth curve. In case of splines you want continuous first derivative, therefore, the roughness is based on the integral of the square of the second derivative: $$\int [f''(x)]^2dx $$

In your case, you could use the second difference which corresponds to the second derivative: $$D2=\sum_i [x_i-2x_{i-1}+x_{i-2}]^2/4$$

Demo

Here's the demo on your data set. For your two series this measure D2 is:

The levels plot:

Here's the second difference plot:

We see the first row is much rougher.

Why not D1?

Let's see why for smoothness (roughness) the second derivative is generally more appropriate.

Consider these two series:

The sums of squares of first differences are the same: 18 The sums of squares of second differences are: 0 and 72, which represents the intuitive and visible roughness very well.

Here's the plot of first difference:

And here's the plot of the second difference:

Conclusion

You can go for higher differences, e.g. third difference, but going after the first difference is not helpful to measure the smoothness. The reason is that our intuitive understanding of smoothness is compatible with any first derivative! Any series with a trend will have the first derivative, and it's not an rough series necessarily. The series are rough when the first derivative starts jumping around, which is when the higher derivatives are high.

Answer 2

If this is an image then in my understanding a row should display a gradual change between the adjacent pixels. In such a case autocorrelation (the correlation of data with itself after a shift by one pixel) should work as a measure of smoothness.

However using your example I only get a slight increase in autocorrelation. Using R:

y1 <- c(118, 117, 118, 120, 80, 117, 118, 120, 118, 119, 121, 119, 121, 118, 121, 120, 118, 80, 120, 121)
y2 <- c(118, 117, 118, 120, 118, 117, 118, 120, 118, 119, 121, 119, 121, 118, 121, 120, 118, 119, 120, 121)

acf(y1, plot=FALSE, lag.max=1)

# Autocorrelations of series ‘y1’, by lag

     0      1
 1.000 -0.095

acf(y2, plot=FALSE, lag.max=1)

# Autocorrelations of series ‘y2’, by lag

    0     1
1.000 0.086

This might happen if there is not much going on in the row you selected. i.e. it only has shades of the same color. Or if the drawing on the picture has very thin edges so that the contours of an object are only one pixel in width. In this case shifting the row by one pixel would dislocate the edges.

Answer 3

One way to measure non-smoothness is to first smooth the data, subtract it away and compute some measure of how much residuals do you have (i.e. sum squares of all residuals). I.e. you can apply a Laplacian filter and compute the sum of squares of the residuals for both images and compare.

Answer 4

I totally agree with @Tim's comment about variance but I felt motivated to go a step further, as is my want. I took the 20 values and mused as to what AUTOBOX would do with these values essentially revisiting this post How to calculate the standard average of a set excluding outliers? .

AUTOBOX delivered the following adjustments to cleanse the data using procedures developed here http://docplayer.net/12080848-Outliers-level-shifts-and-variance-changes-in-time-series.html . Additionally identifying an unusual value at period 4 and a persistant level/step shift starting at period 8.

The plot of the Actual and Cleansed Data is educational as to what the human eye sees and what it doesn't see ..

What we miss initially is the subtle but significant anomaly at period 4 and the persistent level shift at period 8 BECAUSE we are focused on the overwhelming pulse impacts at periods 5 and 18.

Going one step further ( always dangerous with small samples but not necessarily so when there is strong signal ) the model's residuals suggest a constant/persistant blurring (inncreased error variance ) from period 7 to 20

The question I really answered "Is there a better process ?" in terms of making data smoother ? i.e. less effected by blurring . Or is it possible to further reduce the variance (non-systematic behavior )?