Simultaneous heteroscedasticity and heavy tails in a regression model

Question

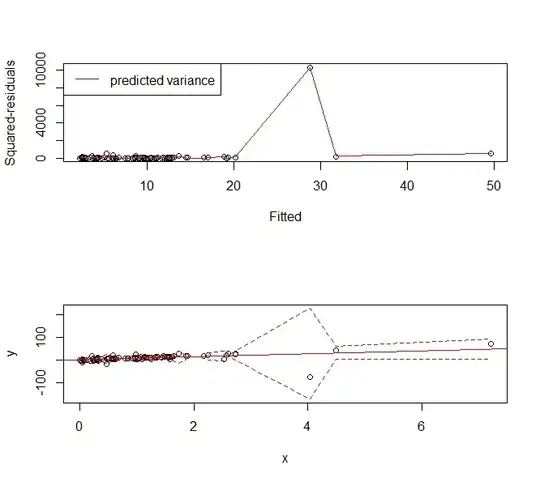
I'm trying to create a prediction model using regression. This is the diagnostic plot for the model that I get from using lm() in R:

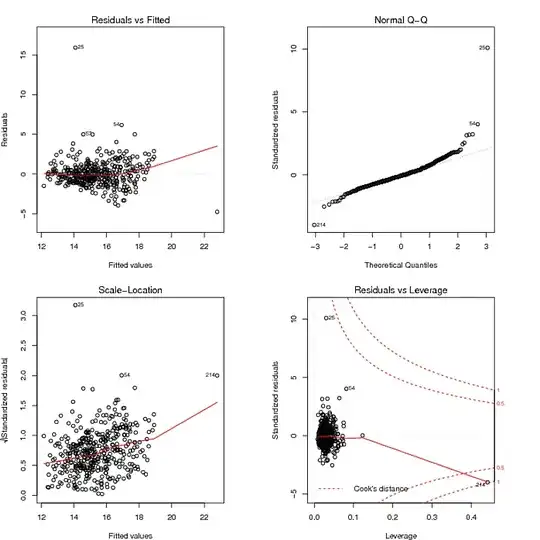
What I read from the Q-Q plot is that the residuals have a heavy-tailed distribution, and the Residuals vs Fitted plot seems to suggest that the variance of the residuals is not constant. I can tame the heavy tails of the residuals by using a robust model:

fitRobust = rlm(formula, method = "MM", data = myData)

But that's where things come to a stop. The robust model weighs several points 0. After I remove those points, this is how the residuals and the fitted values of the robust model look like: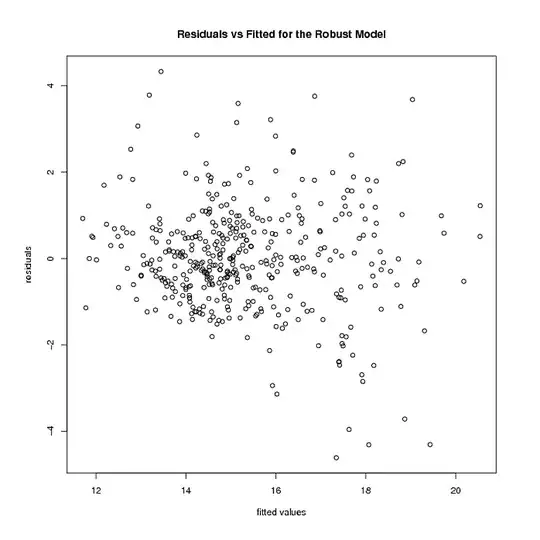

The heteroscedasticity seems to be still there. Using

logtrans(model, alpha) 

from the MASS package, I tried to find an $\alpha$ such that

rlm(formula, method = "MM") 

with formula being $\log(Y + \alpha) \sim X_1+\cdots+X_n$ has residuals with constant variance. Once I find the $\alpha$, the resulting robust model obtained for the above formula has the following Residuals vs Fitted plot:

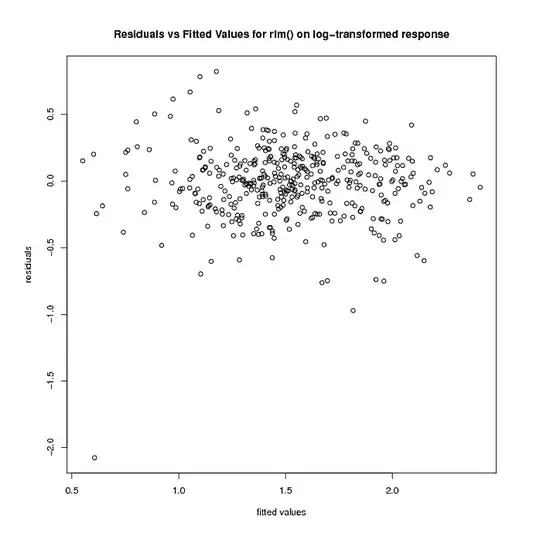
It looks to me as if the residuals still do not have constant variance. I've tried other transformations of response (including Box-Cox), but they don't seem like an improvement either. I am not even sure that the second stage of what I'm doing (i.e. finding a transformation of the response in a robust model) is supported by any theory. I'd very much appreciate any comments, thoughts, or suggestions.

Answer 1

Heteroscedasticity and leptokurtosis are easily conflated in data analysis. Take a data model which generates an error term as Cauchy. This meets the criteria for homoscedasticty. The Cauchy distribution has infinite variance. A Cauchy error is a simulator's way of including an outlier-sampling process.

With these heavy tailed errors, even when you fit the correct mean model, the outlier leads to a large residual. A test of heteroscedasticity has greatly inflated type I error under this model. A Cauchy distribution also has a scale parameter. Generating error terms with a linear increase in scale produces heteroscedastic data, but the power to detect such effects is practically null so the type II error is inflated as well.

Let me suggest then, the proper data analytic approach isn't to become mired in tests. Statistical tests are primarily misleading. No where is this more obvious than tests intended to verify secondary modeling assumptions. They are no substitution for common sense. For your data, you can plainly see two large residuals. Their effect on the trend is minimal as few if any residuals are offset in a linear departure from the 0 line in the plot of residuals vs. fitted. That is all you need to know.

What is desired then is a means of estimating a flexible variance model that will allow you to create prediction intervals over a range of fitted responses. Interestingly, this approach is capable of handling most sane forms of both heteroscedasticity and kurtotis. Why not then use a smoothing spline approach to estimating the mean squared error.

Take the following example:

set.seed(123)
x <- sort(rexp(100))
y <- rcauchy(100, 10*x)

f <- lm(y ~ x)
abline(f, col='red')
p <- predict(f)
r <- residuals(f)^2

s <- smooth.spline(x=p, y=r)

phi <- p + 1.96*sqrt(s$y)
plo <- p - 1.96*sqrt(s$y)

par(mfrow=c(2,1))
plot(p, r, xlab='Fitted', ylab='Squared-residuals')
lines(s, col='red')
legend('topleft', lty=1, col='red', "predicted variance")

plot(x,y, ylim=range(c(plo, phi), na.rm=T))
abline(f, col='red')
lines(x, plo, col='red', lty=2)
lines(x, phi, col='red', lty=2)

Gives the following prediction interval that "widens up" to accommodate the outlier. It is still a consistent estimator of the variance and usefully tells people, "Hey there's this big, wonky observation around X=4 and we can't predict values very usefully there."