An example where the likelihood principle *really* matters?

Question

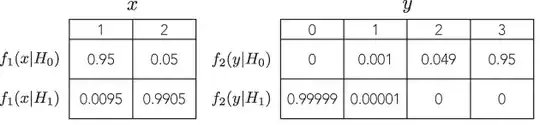
Is there an example where two different defensible tests with proportional likelihoods would lead one to markedly different (and equally defensible) inferences, for instance, where the p-values are order of magnitudes far apart, but the power to alternatives is similar?

All the examples I see are very silly, comparing a binomial with a negative binomial, where the p-value of the first is 7% and of the second 3%, which are "different" only insofar one is making binary decisions on arbitrary thresholds of significance such as 5% (which, by the way, is a pretty low standard for inference) and do not even bother to look at power. If I change the threshold for 1%, for instance, both lead to the same conclusion.

I've never seen an example where it would lead to markedly different and defensible inferences. Is there such an example?

I'm asking because I've seen so much ink spent on this topic, as if the Likelihood Principle is something fundamental in the foundations of statistical inference. But if the best example one has are silly examples like the one above, the principle seems completely inconsequential.

Thus, I'm looking for a very compelling example, where if one does not follow the LP the weight of evidence would be overwhelmingly pointing in one direction given one test, but, in a different test with proportional likelihood, the weight of evidence would be overwhelmingly pointing in an opposite direction, and both conclusions look sensible.

Ideally, one could demonstrate we can have arbitrarily far apart, yet sensible, answers, such as tests with $p =0.1$ versus $p= 10^{-10}$ with proportional likelihoods and equivalent power to detect the same alternative.

PS: Bruce's answer does not address the question at all.

Answer 1

Think about a hypothetical situation when a point null hypothesis is true but one keeps sampling until $p<0.05$ (this will always happen sooner or later, i.e. it will happen with probability 1) and then decides to stop the trial and reject the null. This is an admittedly extreme stopping rule but consider it for the sake of the argument.

This moronic procedure will have 100% Type I error rate, but there is nothing wrong with it according to the Likelihood Principle.

I'd say this does count as "really" mattering. You can of course choose any $\alpha$ in this argument. Bayesians can use a fixed cut-off on Bayes factor if they please. The same logic applies. The main lesson here is that you cannot adhere to LP and have an error rate guarantee. There is no free lunch.

Answer 2

Disclaimer: I believe this answer is at the core of the entire argument, so it worth discussion, but I haven't fully explored the issue. As such, I welcome corrections, refinements and comments.

The most important aspect is in regards to sequentially collected data. For example, suppose you observed binary outcomes, and you saw 10 success and 5 failures. The likelihood principle says that you should come to the same conclusion about the probability of success, regardless of whether you collected data until you had 10 successes (negative binomial) or ran 15 trials, of which 10 were successes (binomial).

Why is this of any importance?

Because according to the likelihood principle (or at least, a certain interpretation of the it), it's totally fine to let the data influence when you're going to stop collecting data, without having to alter your inference tools.

Conflict with Sequential Methods

The idea that using your data to decide when to stop collecting data without altering your inferential tools flies completely in the face of traditional sequential analysis methods. The classic example of this is with methods used in clinical trials. In order to reduce potential exposure to harmful treatments, data is often analyzed at intermediate times before the analysis is done. If the trial hasn't finished yet, but the researchers already have enough data to conclude that the treatment works or is harmful, medical ethics tells us we should stop the trial; if the treatment works, it is ethical to stop the trial and start making the treatment available to non-trial patients. If it is harmful, it is more ethical to stop so that we stop exposing trial patients to a harmful treatment.

The problem is now we've started to do multiple comparisons, so we've increased our Type I error rate if we do not adjust our methods to account for the multiple comparisons. This isn't quite the same as traditional multiple comparisons problems, as it's really multiple partial comparisons (i.e., if we analyze the data once with 50% of the data collected and once with 100%, these two samples clearly are not independent!), but in general the more comparisons we do, the more we need to change our criteria for rejecting the null hypothesis to preserve the type I error rate, with more comparisons planned requiring more evidence to reject the null.

This puts clinical researchers in a dilemma; do you want to frequently check your data, but then increase your required evidence to reject the null, or do you want to infrequently check your data, increasing your power but potentially not acting in an optimal manner in regards to medical ethics (i.e., may delay product to market or expose patients unnecessarily long to harmful treatment).

It is my (perhaps mistaken) understanding that the likelihood principle appears to tell us that it doesn't matter how many times we check the data, we should make the same inference. This basically says that all the approaches to sequential trial design are completely unnecessary; just use the likelihood principle and stop once you've collected enough data to make a conclusion. Since you don't need to alter your inference methods to adjust for the number of analyses you've prepared, there is no trade off dilemma between number of times checked and power. Bam, whole field of sequential analysis is solved (according to this interpretation).

Personally, what is very confusing about this to me is that a fact that is well know in the sequential design field, but fairly subtle, is that the likelihood of the final test statistic is largely altered by the stopping rule; basically, the stopping rules increase the probability in a discontinuous manner at the stopping points. Here is a plot of such a distortion; the dashed line is the PDF of the final test statistic under the null if data is only analyzed after all data is collected, while the solid line gives you the distribution under the null of the test statistic if you check the data 4 times with a given rule.

With that said, it's my understanding that the likelihood principle seems to imply that we can throw out all we know about Frequentist sequential design and forget about how many times we analyze our data. Clearly, the implications of this, especially for the field of clinical designs, is enormous. However, I haven't wrapped my mind around how they justify ignoring how stopping rules alter the likelihood of the final statistic.

Some light discussion can be found here, mostly on the final slides.

Answer 3

Outline of LR tests for exponential data.

Let $X_1, X_2, \dots, X_n$ be a random sample from $\mathsf{Exp}(\text{rate} =\lambda),$ so that $E(X_i) = \mu = 1/\lambda.$ For $x > 0,$ the density function is $f(x) = \lambda e^{-\lambda x}$ and the CDF is $F(x) = 1 - e^{-\lambda x}.$

1. Test statistic is sample minimum.

Let $V = X_{(1)} = \min_n (X_i).$ Then $V \sim \mathsf{Exp}(n\lambda).$ As an outline of the proof, $$P(V > v) = P(X_1 > v, \dots, X_n > v) = \left[e^{-\lambda v}\right]^n= e^{-n\lambda v},$$ so that $P(V \le v) = 1 - e^{-n\lambda v},$ for $v > 0.$

To test $H_9:\mu \le \mu_0$ against $H_a: \mu > \mu_0,$ at level $\alpha = 5\%,$ we regard $V$ as a single observation from its exponential distribution. We find that the log likelihood ratio indicates rejection when $V > c,$ where $P(V > c\, |\, \mu = \mu_0) = 0.05.$

For the specific case in which $n = 100$ and $\mu_0 =10,\, \lambda_0 = 0.1,$ we have exponential rate $10 = n/\mu_0 = 100/10 = 10,$ so that $c = 0.2295$ from R, where the exponential distribution is parameterized by the rate.

 qexp(.95, 10)
 [1] 0.2995732
 1 - pexp(0.2996, 10)
 [1] 0.04998662

Accordingly, the power against the alternative $\mu_a = 100$ (rate $n/\mu_a = 1)$ is about 74%.

1 - pexp(0.2996, 1)
[1] 0.7411146

2. Test statistic is the sample mean.

Oxford U. class notes (second page) show that the likelihood ratio test of $H_0: \mu \le \mu_0$ against $H_0: \mu > \mu_0$ at the 5% level of significance rejects for $\bar X > c,$ where $P(\bar X > c\, |\, \mu = \mu_0) = 0.5.$ Furthermore, one can show using moment generating functions that $\bar X \sim \mathsf{Gamma}(n, n\lambda).$

For the specific case in which $n = 100$ and $\mu_0 =10,\, \lambda_0 = 0.1,$ we have $\bar X \sim \mathsf{Gamma}(100, 10),$ so that $c = 11.7.$

qgamma(.95, 100, 10)
[1] 11.69971
1 - pgamma(11.7, 100, 10)
[1] 0.04997338

Accordingly, power against the alternative $\mu_a = 14$ is about 95.6%.

1 - pgamma(11.7, 100, 100/14)
[1] 0.9562513

Clearly, for purposes of testing hypotheses about the exponential mean $\mu,$ the information in the sufficient statistic $\bar X$ is much greater than the information in the sample minimum.

Answer 4

Violation by different pdf functions $f(x,\theta)$ and $g(x,\theta)$

This case will be an example of 'violation' because the probability distribution functions $f(x,\theta)$ $g(x,\theta)$ are intrinsically different. Even when $f$ and $g$, differ, they may relate to the likelihood principle because at fixed measurement $x$ they give the same functions of $\theta$ up to scaling. The difference, opens up a possibility for "violations".

---

The coin flip with or without optional stopping rule

The coin flip with or without optional stopping rule is a typical example, the pdf is binomial or negative binomial which are different pdf functions and lead to different calculation of p-values, and confidence intervals, but they lead to the same likelihood functions for fixed sample/measurement (up to scaling).

$$\begin{array}{rcrl} f_{\text{Negative Binomial}}(n|k,p) &=& {{n-1}\choose{k-1}}&p^k(1-p)^{n-k} \\ f_{\text{Binomial}}(k|n,p) &=& {{n}\choose{k}}&p^k(1-p)^{n-k} \end{array}$$

---

More extreme example

Consider some measurement of $X$ which is distributed as

$$\mathcal{L}(\theta | x) = f(x|\theta) = \begin{cases} 0 & \text{ if } \quad x < 0 \\a & \text{ if }\quad 0 \geq x < 1 \\ (1-a) \theta \exp(-\theta (x-1)) & \text{ if }\quad x \geq 1 \end{cases}$$

where $a$ is some known parameter that depends on the type of experiment, and $\theta$ is some parameter that may be unknown and could be inferred from the measurement $x$.

For any given $x$ and $a$ the likelihood function is proportional to the same function that is independent from $a$:

• If $x<1$ then $\mathcal{L}(\theta | x) \propto 1$
• If $x\geq 1$ then $\mathcal{L}(\theta | x) \propto \theta \exp(-\theta (x-1))$

But, albeit the same likelihood function, the p-value can vary widely depending on the experiment (ie the value of $a $). For instance when you measure $x=2$ and test $H_0:\theta = 1$ against $H_0:\theta < 1$ then the p-value is

$$P(X>2|\theta = 1) = \frac{(1-a)}{\exp(1)} $$

---

Intuition: The reason for violation in these cases is that p-values and hypothesis tests are not solely based on the likelihood function for the particular observed value $x$.

The p-value is not calculated from the likelihood $f(θ|x)$ with $x$ fixed, but with the pdf $f(x|θ)$ with $θ$ fixed which is a different slice. Confidence intervals, p-value, and hypothesis tests, are different things than the information from likelihood ratios.

p-values are not really evidence: The p-value relates to type I error which is a measure that relates to an ensemble of measurements rather than to a single measurement. This type I error or p-value is not the same as 'evidential meaning' from Birnbaums 'foundations of statistical evidence'. This relates a lot to the problems with p-values and scientist searching for outcomes solely with statistical significance rather than important effects.

Do we need examples where inferences are markedly different? The extreme case is a contrived example. Such a case, or anything with a similar extreme difference, is of course not occurring easily in practice. It is more often the case that the difference will be small such as in the cases that you refer to as silly.

To ask for examples where the likelihood principle 'really matters', or where two different inferences lead to extremely different results, is a bit of a loaded question. At least when the intention for this question relates to some philosophical argument. It is a loaded question because it presupposes that principles that matter should lead to extremely varying results. In many practical cases the results are however small (in terms of different p-values less than an order). I believe that this is not a strange for two different, but both plausible, methods to result in more or less similar results. I would consider the likelihood principle not to be 'less violated' when the differences are only small.

Answer 5

Here is an example adapted from Statistical decision theory and Bayesian analysis by James O. Berger (Second edition page 29).

Say that two species of wasps can be distinguished by the number of notches on the wings (call this $x$) and by the number of black rings around the abdomen (call this $y$). The distribution of the characters in the two species (labelled $H_0$ and $H_1$) are as follows:

Say that we find a specimen with 1 notch on the wings and 1 ring around the abdomen. The weight of evidence if 100 times bigger in favor of $H_1$ against $H_0$ for both characters.

Now if someone wanted to set up a test for $H_0$ at 5% level, the decision rule would be for the first character “accept $H_0$ if there is 1 notch on the wing, otherwise reject it”, and for the second character “accept $H_0$ if there are 3 rings around the abdomen, otherwise reject it”. There are many other possibilities, but these ones are most powerful tests at this level. Yet, they lead to different conclusions for both characters.

---

Note: one could of course set up a test with the rule “accept $H_0$ if there are 1 or 3 rings around the abdomen, otherwise reject it”. The question is whether we prefer a test at 5% level with type II risk 0, or a test at 4.9% level with type II risk 0.00001. The difference is so small that we would probably not care, but as I understand it, this is the core of the argument for the likelihood principle: it is not a good idea to make the result depend on something that seems irrelevant.

---

The likelihood functions are proportional, and yet the p-value of $x = 1$ is 0.95, and that of $y = 1$ is 0.001 (assuming that we reject $H_0$ with events of the form $y \leq \alpha$). It is obvious from the structure of the table that I could have chosen any number smaller than 0.001. Also, the type II risk of the rejection is 0, so it looks like there is nothing “wrong” here.

Still, I admit that this example is somewhat contrived and not completely honest because it plays with the difficulty of arranging tests with discrete data. One could find equivalent examples with continuous data but they would be even more contrived. I agree with the OP that the likelihood principle has almost no practical value; I interpret it as a principle to guarantee some consistency within the theory.