Inverting data for Zero-inflated mixed effects models

Question

I am looking for some advice on my analyses, I have been going back and forth between co-authors about the validity of my approach and would appreciate some external input.

My data are derived from mutli-country household surveys of rural farmers living under different landuse configurations. We are focusing on frequency of food consumption to examine dietary patterns. In order to do so we asked how many days did you consume a particular food group in the last 7 days? (7day recall). I am applying mixed effects models run using the glmmTMB package in R to account for the nested nature of the experimental design. I am happy with this approach but am being questioned as to my logic for using Zero-inflated models. I will explain below and would appreciate any comments, clarifications, suggested alternatives or even a "you cant do that".

There are two main issues I am having with my coauthors.

1. The "inverting" of the data in order to model with a zero-inflated model
2. The assumptions I am making about there being "real" and "structural" zeros and two different processes determining them.

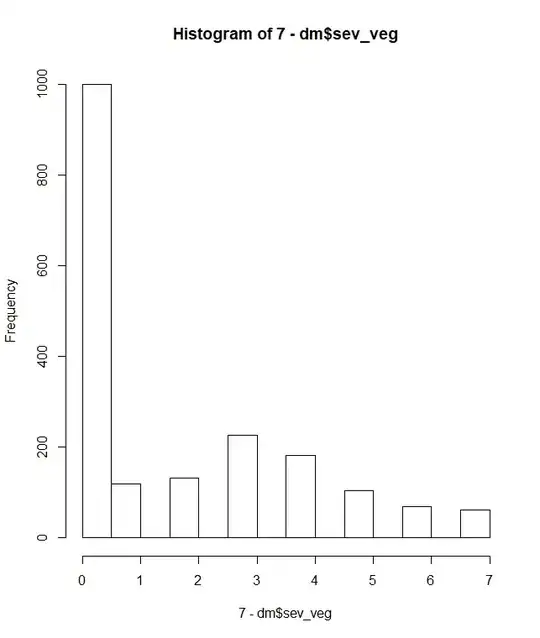
So my data looks like this for meat and vegetable consumption.

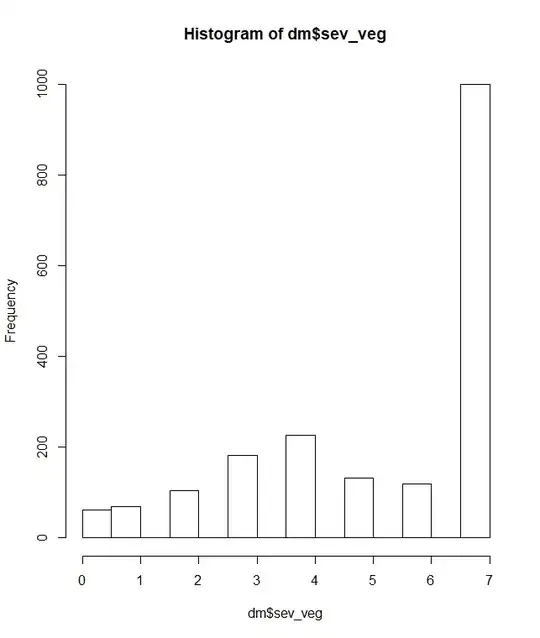
there are obviously lots of people who are eating both food groups 7 days a week and this is potentially inflating the data, especially with the vegetable distribution of counts.

My approach was to "invert" the data so instead it would represent a count of the number of days a respondent went without consuming that food group.

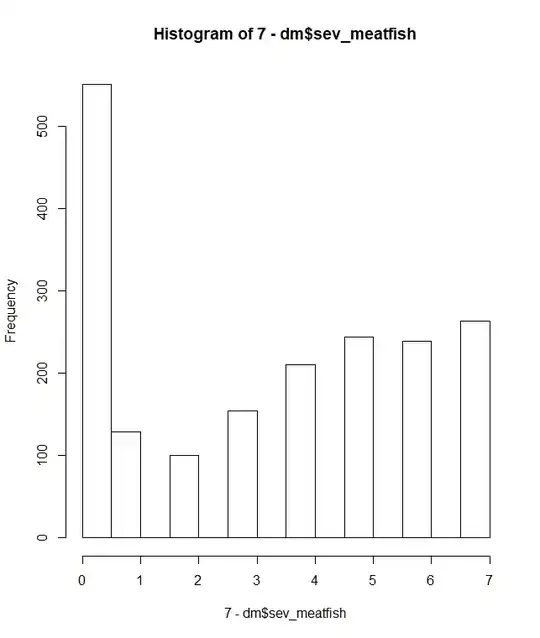
In my mind this makes the data more manageable from a modelling perspective and was my starting point to examining which models would be appropriate.

My first question is: Is it OK to do this from a modelling and statistics point of view?

From here I ran a bunch of models and examined the model fits, the best fits were either zero-inflated Poisson or zero-inflated neg binomial.

The biggest blowback I have been getting (apart from the inverting which I think is fine) is that my coauthors do not agree that there could be two sources of the zeros (which is actually two sources of 7days consumption in its original form before I inverted the data).

I have suggested that there are respondents we surveyed that would always answer 7 days (structural zeros) and respondents that answered 7 days who have a variable weekly intake but just happend to eat 7 days that week (real zeros).

I assume that if people have the the opportunity to eat these food groups daily then they do. So because these people are farmers and have access to these food groups either because they grow them themselves or can readily collect them from the forest or purchase/trade for them by being wealthy enough (all these factors are in controlled for in the model). It seems reasonable to me to assume that some of the people who answered '7 days' are from a group of people that would only ever answer '7 days' (structural zeros) and therefore the zero-inflated models are appropriate, remembering that because I inverted the data a structural zero actually means being from the group of people who could only ever answer zero days without consumption of that particular food group. So there is one set of processes that determines the odds of one someone only being able (close enough to only) to answer 7days and another set of processes that determine the frequency of consumption for those who cannot only answer 7days.

My second question is: Is this approach appropriate and does it justify the use of zero inflated models?

I would really appreciate people to point out any flaws in my approach or my logic and suggest alternatives or point me in the direction of alternative approaches. I have looked into quite a few different approaches and I always end up back here.

It should be noted that the outputs from the models make perfect sense in terms of the significant factors driving each process for real and structural zeros(I would be worried if they were throwing weird results).

Many thanks in advance!

Answer 1

The negative binomial model is typically used for count data with no upper limit, i.e., the outcome variable $Y$ can take values in the set $[0, 1, 2, \ldots, \infty)$. However, in your case you can only have a maximum count of 7.

A more appropriate distribution for your data is the binomial distribution, which describes the number of “successes” (i.e., in your case success = eating meat & vegetables) in $N$ trials (i.e., in your case $N = 7$ is the number of days).

P.s., note that in both cases of negative binomial and Binomial mixed models you need to be careful with the interpretation of the estimated fixed-effects coefficients; for more details on this check this post.