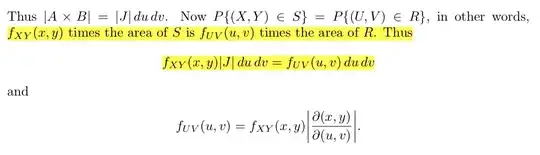I found a good lecture about Jacobian Matrix which was part of a statistics course. However, it was published 20 years ago and lack of explanation. As a beginner of statistics, I'm not able to find the relation between $f_{XY}, f_{UV}$ and respective area.
Can anyone help me understand the highlighted text? I've attached a screenshot of the lecture in the following. You can also find the original lecture from the bottom link.
https://faculty.math.illinois.edu/~r-ash/Stat/StatLec1-5.pdf