The Book of Why by Judea Pearl: Why is he bashing statistics?

Question

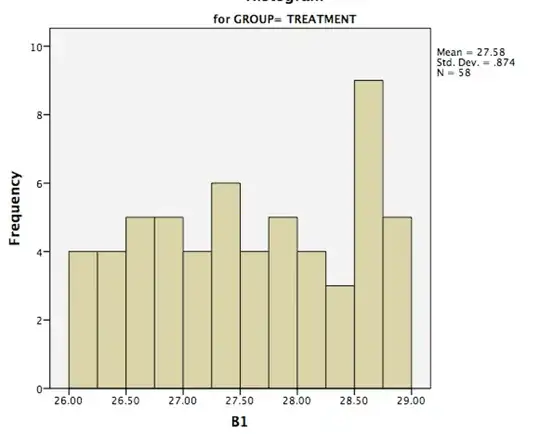
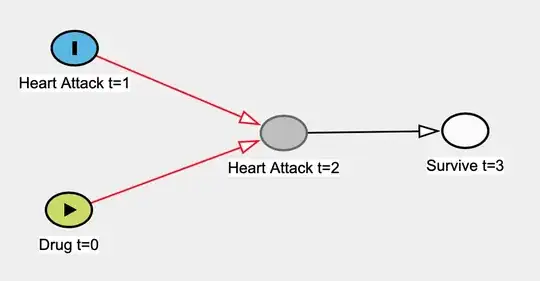
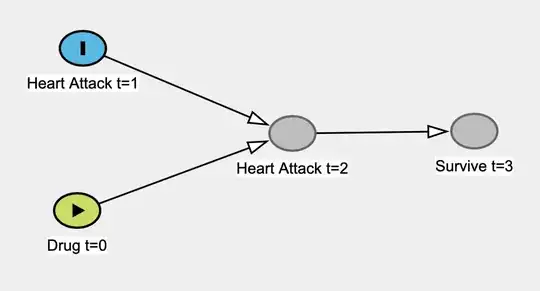
I am reading The Book of Why by Judea Pearl, and it is getting under my skin¹. Specifically, it appears to me that he is unconditionally bashing "classical" statistics by putting up a straw man argument that statistics is never, ever able to investigate causal relations, that it never is interested in causal relations, and that statistics "became a model-blinded data-reduction enterprise". Statistics becomes an ugly s-word in his book.

For example:

Statisticians have been immensely confused about what variables should and should not be controlled for, so the default practice has been to control for everything one can measure. [...] It is a convenient, simple procedure to follow, but it is both wasteful and ridden with errors. A key achievement of the Causal Revolution has been to bring an end to this confusion.

At the same time, statisticians greatly underrate controlling in the sense that they are loath to talk about causality at all [...]

However, causal models have been in statistics like, forever. I mean, a regression model can be used essentially a causal model, since we are essentially assuming that one variable is the cause and another is the effect (hence correlation is different approach from regression modelling) and testing whether this causal relationship explains the observed patterns.

Another quote:

No wonder statisticians in particular found this puzzle [The Monty Hall problem] hard to comprehend. They are accustomed to, as R.A. Fisher (1922) put it, "the reduction of data" and ignoring the data-generating process.

This reminds me of the reply Andrew Gelman wrote to the famous xkcd cartoon on Bayesians and frequentists: "Still, I think the cartoon as a whole is unfair in that it compares a sensible Bayesian to a frequentist statistician who blindly follows the advice of shallow textbooks."

The amount of misrepresentation of s-word which, as I perceive it, exists in Judea Pearls book made me wonder whether causal inference (which hitherto I perceived as a useful and interesting way of organizing and testing a scientific hypothesis²) is questionable.

Questions: do you think that Judea Pearl is misrepresenting statistics, and if yes, why? Just to make causal inference sound bigger than it is? Do you think that causal inference is a Revolution with a big R which really changes all our thinking?

Edit:

The questions above are my main issue, but since they are, admittedly, opinionated, please answer these concrete questions (1) what is the meaning of the "Causation Revolution"? (2) how is it different from "orthodox" statistics?

<sub>1. Also because he is such a modest guy.
2. I mean in the scientific, not statistical sense.</sub>

EDIT: Andrew Gelman wrote this blog post on Judea Pearls book and I think he did a much better job explaining my problems with this book than I did. Here are two quotes:

On page 66 of the book, Pearl and Mackenzie write that statistics “became a model-blind data reduction enterprise.” Hey! What the hell are you talking about?? I’m a statistician, I’ve been doing statistics for 30 years, working in areas ranging from politics to toxicology. “Model-blind data reduction”? That’s just bullshit. We use models all the time.

And another one:

Look. I know about the pluralist’s dilemma. On one hand, Pearl believes that his methods are better than everything that came before. Fine. For him, and for many others, they are the best tools out there for studying causal inference. At the same time, as a pluralist, or a student of scientific history, we realize that there are many ways to bake a cake. It’s challenging to show respect to approaches that you don’t really work for you, and at some point the only way to do it is to step back and realize that real people use these methods to solve real problems. For example, I think making decisions using p-values is a terrible and logically incoherent idea that’s led to lots of scientific disasters; at the same time, many scientists do manage to use p-values as tools for learning. I recognize that. Similarly, I’d recommend that Pearl recognize that the apparatus of statistics, hierarchical regression modeling, interactions, poststratification, machine learning, etc etc., solves real problems in causal inference. Our methods, like Pearl’s, can also mess up—GIGO!—and maybe Pearl’s right that we’d all be better off to switch to his approach. But I don’t think it’s helping when he gives out inaccurate statements about what we do.

Answer 1

Your very question reflects what Pearl is saying!

a simple linear regression is essentially a causal model

No, a linear regression is a statistical model, not a causal model. Let's assume $Y, X, Z$ are random variables with a multivariate normal distribution. Then you can correctly estimate the linear expectations $E[Y\mid X]$, $E[X\mid Y]$, $E[Y\mid X,Z]$, $E[Z\mid Y, X]$ etc using linear regression, but there's nothing here that says whether any of those quantities are causal.

A linear structural equation, on the other hand, is a causal model. But the first step is to understand the difference between statistical assumptions (constraints on the observed joint probability distribution) and causal assumptions (constraints on the causal model).

do you think that Judea Pearl misrepresenting statistics, and if yes, why?

No, I don't think so, because we see these misconceptions daily. Of course, Pearl is making some generalizations, since some statisticians do work with causal inference (Don Rubin was a pioneer in promoting potential outcomes... also, I am a statistician!). But he is correct in saying that the bulk of traditional statistics education shuns causality, even to formally define what a causal effect is.

To make this clear, if we ask a statistician/econometrician with just a regular training to define mathematically what is the expected value of $Y$ if we intervene on $X$, he would probably write $E[Y|X]$ (see an example here)! But that's an observational quantity, that's not how you define a causal effect! In other terms, currently, a student with just a traditional statistics course lacks even the ability of properly defining this quantity mathematically ($E[Y_{x}]$ or $E[Y|do(x)]$) if you are not familiar with the structural/counterfactual theory of causation!

The quote you bring from the book is also a great example. You will not find in traditional statistics books a correct definition of what a confounder is, nor guidance about when you should (or should not) adjust for a covariate in observational studies. In general, you see “correlational criteria”, such as “if the covariate is associated with the treatment and with the outcome, you should adjust for it”. One of the most notable examples of this confusion shows up in Simpson’s Paradox—when faced with two estimates of opposite signs, which one should you use, the adjusted or unadjusted? The, answer, of course, depends on the causal model.

And what does Pearl mean when he says that this question was brought to an end? In the case of simple adjustment via regression, he is referring to the backdoor criterion (see more here). And for identification in general---beyond simple adjustment---he means that we now have complete algorithms for identification of causal effects for any given semi-markovian DAG.

Another remark here is worth making. Even in experimental studies — where traditional statistics has surely done a lot of important work with the design of experiments!— in the end of the day you still need a causal model. Experiments can suffer from lack of compliance, from loss of follow up, from selection bias... also, most of the time you don't want to confine the results of your experiments to the specific population you analyzed, you want to generalize your experimental results to a broader/different population. Here, again, one may ask: what should you adjust for? Are the data and substantive knowledge you have enough to allow such extrapolation? All of these are causal concepts, thus you need a language to formally express causal assumptions and check whether they are enough to allow you to do what you want!

In sum, these misconceptions are widespread in statistics and econometrics, there are several examples here in Cross Validated, such as:

• understanding what a confounder is
• understanding which variables you should include in a regression (for estimating causal effects)
• understanding that even if you include all variables a regression may not be causal
• understanding the difference between (lack of) statistical associations and causation
• defining a causal model and causal effects

And many more.

Do you think that causal inference is a Revolution with a big R which really changes all our thinking?

Considering the current state of affairs in many sciences, how much we have advanced and how fast things are changing, and how much we can still do, I would say this is indeed a revolution.

PS: Pearl suggested two of his posts on UCLA's causality blog that will be of interest to this discussion, you can find the posts here and here.

PS 2: As January has mentioned in his new edit, Andrew Gelman has a new post in his blog. In addition to the debate on Gelman's blog, Pearl has also answered on twitter (below):

Gelman's review of #Bookofwhy should be of interest because it represents an attitude that paralyzes wide circles of statistical researchers. My initial reaction is now posted on https://t.co/mRyDcgQtEc Related posts: https://t.co/xUwR6eCGrZ and https://t.co/qwqV3oyGUy

— Judea Pearl (@yudapearl) January 9, 2019

Answer 2

I fully agree that Pearl's tone is arrogant, and his characterisation of "statisticians" is simplistic and monolithic. Also, I don't find his writing particularly clear.

However, I think he has a point.

Causal reasoning was not part of my formal training (MSc): the closest I got to the topic was an elective course in experimental design, i.e. any causality claims required me to physically control the environment. Pearl's book Causality was my first exposure to a refutation of this idea. Obviously I can't speak for all statisticians and curricula, but from my own perspective I subscribe to Pearl's observation that causal reasoning is not a priority in statistics.

It is true that statisticians sometimes control for more variables than is strictly necessary, but this rarely leads to error (at least in my experience).

This is also a belief that I held after graduating with an MSc in statistics in 2010.

However, it is deeply incorrect. When you control for a common effect (called "collider" in the book), you can introduce selection bias. This realization was quite astonishing to me, and really convinced me of the usefulness of representing my causal hypotheses as graphs.

EDIT: I was asked to elaborate on selection bias. This topic is quite subtle, I highly recommend perusing the edX MOOC on Causal Diagrams, a very nice introduction to graphs which has a chapter dedicated to selection bias.

For a toy example, to paraphrase this paper cited in the book: Consider the variables A=attractiveness, B=beauty, C=competence. Suppose that B and C are causally unrelated in the general population (i.e., beauty does not cause competence, competence does not cause beauty, and beauty and competence do not share a common cause). Suppose also that any one of B or C is sufficient for being attractive, i.e. A is a collider. Conditioning on A creates a spurious association between B and C.

A more serious example is the "birth weight paradox", according to which a mother's smoking (S) during pregnancy seems to decrease the mortality (M) of the baby, if the baby is underweight (U). The proposed explanation is that birth defects (D) also cause low birth weight, and also contribute to mortality. The corresponding causal diagram is { S -> U, D -> U, U -> M, S -> M, D -> M } in which U is a collider; conditioning on it introduces the spurious association. The intuition behind this is that if the mother is a smoker, the low birth weight is less likely to be due to a defect.

Answer 3

I'm a fan of Judea's writing, and I've read Causality (love) and Book of Why (like).

I do not feel that Judea is bashing statistics. It's hard to hear criticism. But what can we say about any person or field that doesn't take criticism? They tend from greatness to complacency. You must ask: is the criticism correct, needed, useful, and does it propose alternatives? The answer to all those is an emphatic "Yes".

Correct? I've reviewed and collaborated on a few dozen papers, mostly analyses of observational data, and I rarely feel there is a sufficient discussion of causality. The "adjustment" approach involves selecting variables because they were hand-picked from the DD as being "useful" "relevant" "important" or other nonsense.$^1$

Needed? The media is awash with seemingly contradictory statements about the health effects of major exposures. Inconsistency with data analysis has stagnated evidence which leaves us lacking useful policy, healthcare procedures, and recommendations for better living.

Useful? Judea's comment is pertinent and specific enough to give pause. It is directly relevant to any data analysis any statistician or data expert might encounter.

Does it propose alternatives? Yes, Judea in fact discusses the possibility of advanced statistical methods, and even how they reduce to known statistical frameworks (like Structural Equation Modeling) and their connection to regression models). It all boils down to requiring an explicit statement of the content knowledge that has guided the modeling approach.

Judea isn't simply suggesting we defenestrate all statistical methods (e.g. regression). Rather, he is saying that we need to embrace some causal theory to justify models.

$^1$ the complaint here is about the use of convincing and imprecise language to justify what is ultimately the wrong approach to modeling. There can be overlap, serendipitously, but Pearl is clear about the purpose of a causal diagram (DAG) and how variables can be classified as "confounders".

Answer 4

I haven't read this book, so I can only judge the particular quote you give. However, even on this basis, I agree with you that this seems extremely unfair to the statistical profession. I actually think that statisticians have always done a remarkably good job at stressing the distinction between statistical associations (correlation, etc.) and causality, and warning against the conflation of the two. Indeed, in my experience, statisticians have generally been the primary professional force fighting against the ubiquitous confusion between cause and correlation. It is outright false (and virtually slander) to claim that statisticians are "...loath to talk about causality at all." I can see why you are annoyed reading arrogant horseshit like this.

I would say that it is reasonably common for non-statisticians who use statistical models to have a poor understanding of the relationship between statistical association and causality. Some have good scientific training from other fields, in which case they may also be well aware of the issue, but there are certainly some people who use statistical models who have a poor grasp of these issues. This is true in many applied scientific fields where practitioners have basic training in statistics, but do not learn it at a deep level. In these cases it is often professional statisticians who alert other researchers to the distinctions between these concepts and their proper relationship. Statisticians are often the key designers of RCTs and other experiments involving controls used to isolate causality. They are often called on to explain protocols such as randomisation, placebos, and other protocols that are used to try to sever relationships with potential confounding variables. It is true that statisticians sometimes control for more variables than is strictly necessary, but this rarely leads to error (at least in my experience). I think most statisticians are aware of the difference between confounding variables and collider variables when they do regression analysis with a view to causal inferences, and even if they are not always building perfect models, the notion that they somehow eschew consideration of causality is simply ridiculous.

I think Judea Pearl has made a very valuable contribution to statistics with his work on causality, and I am grateful to him for this wonderful contribution. He has constructed and examined some very useful formalisms that help to isolate causal relationships, and his work has become a staple of a good statistical education. I read his book Causality while I was a grad student, and it is on my shelf, and on the shelves of many other statisticians. Much of this formalism echoes things that have been known intuitively to statisticians since before they were formalised into an algebraic system, but it is very valuable in any case, and goes beyond that which is obvious. (I actually think in the future we will see a merging of the "do" operation with probability algebra occurring at an axiomatic level, and this will probably eventually become the core of probability theory. I would love to see this built directly into statistical education, so that you learn about causal models and the "do" operation when you learn about probability measures.)

One final thing to bear in mind here is that there are many applications of statistics where the goal is predictive, where the practitioner is not seeking to infer causality. These types of applications are extremely common in statistics, and in such cases, it is important not to restrict oneself to causal relationships. This is true in most applications of statistics in finance, HR, workforce modelling, and many other fields. One should not underestimate the amount of contexts where one cannot or should not seek to control variables.

---

Update: I notice that my answer disagrees with the one provided by Carlos. Perhaps we disagree on what constitutes "a statistician/econometrician with just a regular training". Anyone who I would call a "statistician" usually has at least a graduate-level education, and usually has substantial professional training/experience. (For example, in Australia, the requirement to become an "Accredited Statistician" with our national professional body requires a minimum of four years experience after an honours degree, or six years experience after a regular bachelors degree.) In any case, a student studying statistics is not a statistician.

I notice that as evidence of the alleged lack of understanding of causality by statisticians, Carlos's answer points to several questions on CV.SE which ask about causality in regression. In every one of these cases, the question is asked by someone who is obviously a novice (not a statistician) and the answers given by Carlos and others (which reflect the correct explanation) are highly-upvoted answers. Indeed, in several of the cases Carlos has given a detailed account of the causality and his answers are the most highly up-voted. This surely proves that statisticians do understand causality.

Some other posters have pointed out that analysis of causality is often not included in the statistics curriculum. That is true, and it is a great shame, but most professional statisticians are not recent graduates, and they have learned far beyond what is included in a standard masters program. Again, in this respect, it appears that I have a higher view of the average level of knowledge of statisticians than other posters.

Answer 5

a simple linear regression is essentially a causal model

Here's an example I came up with where a linear regression model fails to be causal. Let's say a priori that a drug was taken at time 0 (t=0) and that it has no effect on the rate of heart attacks at t=1. Heart attacks at t=1 affect heart attacks at t=2 (i.e. previous damage makes the heart more susceptible to damage). Survival at t=3 only depends on whether or not people had a heart attack at t=2 -- heart attack at t=1 realistically would affect survival at t=3, but we won't have an arrow, for the sake of simplicity.

Here's the legend:

Here's the true causal graph:

Let's pretend that we don't know that heart attacks at t=1 are independent of taking the drug at t=0 so we construct a simple linear regression model to estimate the effect of the drug on heart attack at t=0. Here our predictor would be Drug t=0 and our outcome variable would be Heart Attack t=1. The only data we have is people who survive at t=3, so we'll run our regression on that data.

Here's the 95% Bayesian credible interval for coefficient of Drug t=0:

Much of the probability as we can see is greater than 0, so it looks like there's an effect! However, we know a priori that there is 0 effect. The mathematics of causation as developed by Judea Pearl and others make it much easier to see that there will be bias in this example (due to conditioning on a descendant of a collider). Judea's work implies that in this situation, we should use the full data set (i.e. don't look at the people who only survived), which will remove the biased paths:

Here's the 95% Credible Interval when looking at the full data set (i.e. not conditioning on those who survived).

.

It is densely centered at 0, which essentially shows no association at all.

In real-life examples, things might not be so simple. There may be many more variables that might cause systematic bias (confounding, selection bias, etc.). What to adjust for in analyses has been mathematized by Pearl; algorithms can suggest which variable to adjust for, or even tell us when adjusting is not enough to remove systematic bias. With this formal theory set in place, we don't need to spend so much time arguing about what to adjust for and what not to adjust for; we can quickly reach conclusions as to whether or not our results are sound. We can design our experiments better, we can analyze observational data more easily.

Here's a freely-available course online on Causal DAGs by Miguel Hernàn. It has a bunch of real-life case studies where professors / scientists / statisticians have come to opposite conclusions about the question at hand. Some of them might seem like paradoxes. However, you can easily solve them via Judea Pearl's d-separation and backdoor-criterion.

For reference, here's code to the data-generating process and the code for credible intervals shown above:

import numpy as np
import pandas as pd
import statsmodels as sm
import pymc3 as pm
from sklearn.linear_model import LinearRegression

%matplotlib inline

# notice that taking the drug is independent of heart attack at time 1.
# heart_attack_time_1 doesn't "listen" to take_drug_t_0
take_drug_t_0 = np.random.binomial(n=1, p=0.7, size=10000)
heart_attack_time_1 = np.random.binomial(n=1, p=0.4, size=10000)

proba_heart_attack_time_2 = []

# heart_attack_time_1 increases the probability of heart_attack_time_2. Let's say
# it's because it weakens the heart and makes it more susceptible to further
# injuries
# 
# Yet, take_drug_t_0 decreases the probability of heart attacks happening at
# time 2
for drug_t_0, heart_attack_t_1 in zip(take_drug_t_0, heart_attack_time_1):
    if drug_t_0 == 0 and heart_attack_t_1 == 0:
        proba_heart_attack_time_2.append(0.1)
    elif drug_t_0 == 1 and heart_attack_t_1 == 0:
        proba_heart_attack_time_2.append(0.1)
    elif drug_t_0 == 0 and heart_attack_t_1 == 1:
        proba_heart_attack_time_2.append(0.5)
    elif drug_t_0 == 1 and heart_attack_t_1 == 1:
        proba_heart_attack_time_2.append(0.05)

heart_attack_time_2 = np.random.binomial(
    n=2, p=proba_heart_attack_time_2, size=10000
)

# people who've had a heart attack at time 2 are more likely to die by time 3

proba_survive_t_3 = []
for heart_attack_t_2 in heart_attack_time_2:
    if heart_attack_t_2 == 0:
        proba_survive_t_3.append(0.95)
    else:
        proba_survive_t_3.append(0.6)

survive_t_3 = np.random.binomial(
    n=1, p=proba_survive_t_3, size=10000
)

df = pd.DataFrame(
    {
        'survive_t_3': survive_t_3,
        'take_drug_t_0': take_drug_t_0,
        'heart_attack_time_1': heart_attack_time_1,
        'heart_attack_time_2': heart_attack_time_2
    }
)

# we only have access to data of the people who survived
survive_t_3_data = df[
    df['survive_t_3'] == 1
]

survive_t_3_X = survive_t_3_data[['take_drug_t_0']]

lr = LinearRegression()
lr.fit(survive_t_3_X, survive_t_3_data['heart_attack_time_1'])
lr.coef_

with pm.Model() as collider_bias_model_normal:
    alpha = pm.Normal(name='alpha', mu=0, sd=1)
    take_drug_t_0 = pm.Normal(name='take_drug_t_0', mu=0, sd=1)
    summation = alpha + take_drug_t_0 * survive_t_3_data['take_drug_t_0']
    sigma = pm.Exponential('sigma', lam=1)           

    pm.Normal(
        name='observed', 
        mu=summation,
        sd=sigma,
        observed=survive_t_3_data['heart_attack_time_1']
    )

    collider_bias_normal_trace = pm.sample(2000, tune=1000)

pm.plot_posterior(collider_bias_normal_trace['take_drug_t_0'])

with pm.Model() as no_collider_bias_model_normal:
    alpha = pm.Normal(name='alpha', mu=0, sd=1)
    take_drug_t_0 = pm.Normal(name='take_drug_t_0', mu=0, sd=1)
    summation = alpha + take_drug_t_0 * df['take_drug_t_0']
    sigma = pm.Exponential('sigma', lam=1)           

    pm.Normal(
        name='observed', 
        mu=summation,
        sd=sigma,
        observed=df['heart_attack_time_1']
    )

    no_collider_bias_normal_trace = pm.sample(2000, tune=2000)

pm.plot_posterior(no_collider_bias_normal_trace['take_drug_t_0'])

Answer 6

Two papers, the second a classic, that help (I think) shed additional lights on Judea's points and this topic more generally. This comes from someone who has used SEM (which is correlation and regression) repeatedly and resonates with his critiques:

https://www.sciencedirect.com/science/article/pii/S0022103111001466

http://psycnet.apa.org/record/1973-20037-001

Essentially the papers describe why correlational models (regression) can not ordinarily be taken as implying any strong causal inference. Any pattern of associations can fit a given covariance matrix (i.e., non specification of direction and or relationship among the variables). Hence the need for such things as an experimental design, counterfactual propositions, etc. This even applies when one has a temporal structure to their data where the putative cause occurs in time before the putative effect.

Answer 7

"...since we are essentially assuming that one variable is the cause and another is the effect (hence correlation is different approach from regression modelling)..."

Regression modeling most definitely does NOT make this assumption.

"... and testing whether this causal relationship explains the observed patterns."

If you are assuming causality and validating it against observations, your are doing SEM modeling, or what Pearl would call SCM modeling. Whether or not you want to call that part of the domain of stats is debatable. But I think most wouldn't call it classical stats.

Rather than dumping on stats in general, I believe Pearl is just criticizing statistician's reticence to address causal semantics. He considers this a serious problem because of what Carl Sagan calls the "get in and get out" phenomenon, where you drop a study that says "meat consumption 'strongly associated' with increased libido, p < .05" and then bows out knowing full well the two outcomes are going to be causally linked in the mind of the public.