1

Consider a problem:

You take a fair die to a party and announce that you will roll it 25 times.

You will record each outcome and at the end average the 25 outcomes together to get their arithmetical mean.

You offer a bet: The player puts down \$1. If mean exceeds 4, you will give him $21 back, but otherwise, he loses his dollar. Is this a good bet for the player?

(Use Central limit theorem, CTL).

I tried to solve it. Please check whether it is true: Solution

Community
  • 1
Hassan Ali
  • 31
  • 1
  • 6
  • @MartijnWeterings This is very obviously a copy-pasted problem from somewhere. I took the liberty to change the formatting to reflect that and to add the [self-study] tag. (Your answer is great, btw.) – amoeba Nov 13 '18 at 10:01

2 Answers2

8

You are effectively taking the probability for a single dice roll being larger than 4 (which is indeed $\frac{1}{3}$). But that is a different thing than the mean of several dice rolls being larger than 4 (you can express this also as the sum of $x$ dice rolls being larger than $4x$).

Here I will provide an intuition behind the reason for your error by using the case of two dice rolls. Then I plot some further examples with more dice rolls to see what happens for even larger numbers. And eventually you will see that an approximation with the Normal distribution will be a good idea (although for 25 dice rolls you can also still calculate it exactly).

Two dice rolls example

The probabilities for the mean of dice rolls being above some number is not the same as the probability for a single dice roll being above some number. $P(\bar{x}_{\text{multiple rolls}}>4) \neq P(x_{\text{single roll}}>4)$

See for instance the possible outcomes of two dice rolls, where only $\frac{10}{36} < \frac{1}{3}$ have a mean above 4 (or total above 8)

$$\begin{array}{c|ccccc} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 4 & 5 & 6 & 7 & 8 & \color{red}9 \\ 4 & 5 & 6 & 7 & 8 & \color{red}9 & \color{red}{10} \\ 5 & 6 & 7 & 8 & \color{red}9 & \color{red}{10} & \color{red}{11}\\ 6 & 7 & 8 & \color{red}9 & \color{red}{10} & \color{red}{11} & \color{red}{12} \end{array}$$

More dice rolls

The image below shows how this continues for more dice rolls, by plotting the probability of the sum of dice rolls $X$.

dice rolls example

25 dice rolls

  • Explicit: You can calculate this explicitly by computing a table like above for the two dice rolls, but then for many instead. There has already been a question about this on this site (How to easily determine the results distribution for multiple dice?). Such calculation will give you a probability of: $$P(\bar{x}>4) = \frac{1823148354623298816}{6^{25}} \approx 0.0641 > \frac{1}{21} $$

  • Approximation with normal distribution: In the image above you might note the bell shape curve of the normal distribution. The normal distribution is actually a quite good approximation for the mean of a dice roll (in fact the normal distribution was first described in relation to the approximation of coin flips, where deMoivre used a precursor of the normal distribution to approximated the binomial distribution, and you might see the dice roll as a multivariate generalization of the coin flip).

    This is 'what the question wants you to do': Use the normal distribution as an approximation for the mean of dice rolls. (and then use the resulting expression for the normal distribution to compute $P(\bar{x}>4)$). The question mentions CLT (the central limit theorem), and when you look that up you may find expressions for "approximating the mean of a sample based on the variance of the distribution" (if one would be pedantic then one could say that this approximation is not exactly the same as the 'central limit theorem', but many people mention/use this term when they employ this type of approximation).

    See the image below how the exact probability compares to the approximation with the normal distribution. The image on the right is the same function but plotted on a logarithmic scale to better show the difference. It seems only a slight difference but the true value and the estimated value for $P(\bar{x}>4)$ will be different by about 12 percent.

comparison 25 dice rolls with normal distribution approximation

Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161
  • I am little confused that you use two dies or two rolls of a single die.In my question we roll single die 25 times – Hassan Ali Nov 12 '18 at 18:11
  • @HassanAli I *use* two dies as *simplified* example for changes that occur when you go from one dice roll to a mean of multiple dice rolls. In this way you can more intuitively get an overview of what happens when you take the mean of 25 dice rolls. The example with the two dice rolls show explicitly how your calculation of $P(\bar{x}>4) = 1/3$ is wrong. Note that the answer contains a link to [how to easily determine the results distribution for multiple dice](https://stats.stackexchange.com/questions/3614/) (although the aim of your question seems to be that you use the normal distribution) – Sextus Empiricus Nov 12 '18 at 19:34
  • Wetering So can i use similar process to anwer my question because i think the answer can be logical only using the above P(x¯>4)=0.0641 that player shouldn't bet or bet isn't good for player. – Hassan Ali Nov 13 '18 at 04:14
  • @HassanAli I do not understand what you mean by *"because i think the answer can be logical only using the above..."*. Anyway the example of two dice rolls is just to get an intuitive idea about the question. Mathematicians do this very often. First simplify the problem to gain an understanding and then go to the full scale problem. In my answer I (1) show how in the case of two dice rolls your method does not work (the probability is not 1/3 but instead 10/36) (2) then we increase the number of dice rolls and we observe that the distribution approaches the shape of the normal distribution. – Sextus Empiricus Nov 13 '18 at 08:50
  • For your question you will still need to apply the approximation with the normal distribution (that is the idea, didactic goal, of this homework). It will give you an answer for $P(\bar{x}>4)$ that will be roughly 12% different from the exact answer. – Sextus Empiricus Nov 13 '18 at 09:08
4

I have some hints for you and I suggest you work from there. I might have made errors as well. If you need more help or find an error, leave a comment.

First we write the probability mass function for a having the result $N$ on a single die:

$$prob(N_i)=1/6,\, \text{with }N=1,2,3,4,5,6$$

This is a Discrete Uniform Distribution. All results are equally likely since the die is fair. Now consider the result of summing the faces of 25 rolls of the die and taking the average. The average $S$ is given by the sum of $N_i$ with $i=1,...25$ over 25 where the $N_i$ are i.i.d. distributed as above.

$$S= \frac{N_1 + N_2 + ... +N_{25}}{25}$$

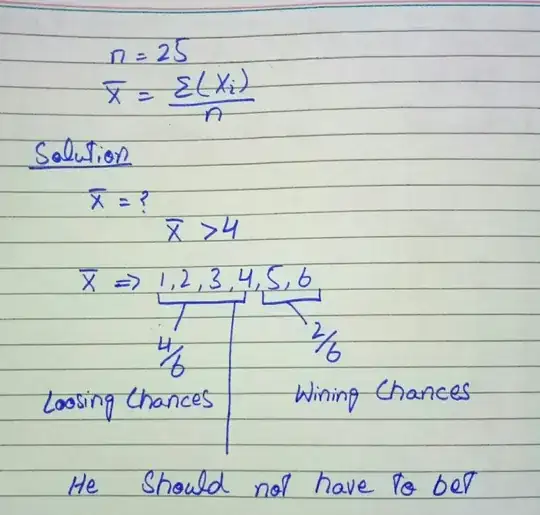
So we ask what is $prob(S>4)$.

For that you first need the probability distribution of $S$. Here is where the hint with the Central Limit Theorem comes in handy. It tells us that we can approximate the density of $prob(S)$ can be approximated as Gaussian with

$$prob(S) \sim \mathcal{N}(\mu,\sigma^2/25)$$

where $\mu$ is the expected value of the uniform distribution from above and $\sigma^2$ is its variance. You can calculate them using the information on this Wikipedia page.

EDIT If you do not want to use the Gaussian approximation, have a look at the Bates Distribution as suggested by @wolfies.

Do you think you can take it from here?

geo
  • 362
  • 3
  • 9
  • I think we should make him do it without the CLT: the question asks what is the probability -- not what is the approximate probability. – wolfies Nov 12 '18 at 10:20
  • @wolfies In that case I suggest Hassan should have a look at [the Irwin-Hall distribution](https://en.wikipedia.org/wiki/Irwin%E2%80%93Hall_distribution). I just assumed the CLT part was part of the assignment. – geo Nov 12 '18 at 10:41
  • 1
    Or the Bates distribution (for the sample mean) – wolfies Nov 12 '18 at 10:54
  • @wolfies Thanks, I have edited my answer to include the Bates distribution. I incorrectly suggested the Irwin-Hall. – geo Nov 12 '18 at 11:20