How do children manage to pull their parents together in a PCA projection of a GWAS data set?

Question

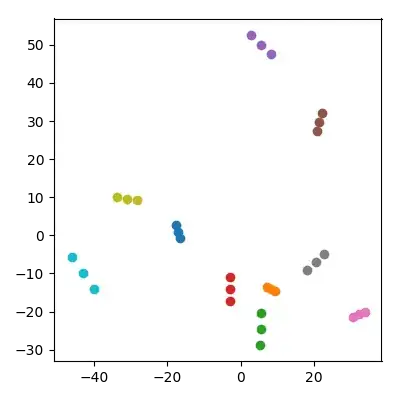
Take 20 random points in a 10,000-dimensional space with each coordinate iid from $\mathcal N(0,1)$. Split them into 10 pairs ("couples") and add the average of each pair ("a child") to the dataset. Then do PCA on the resulting 30 points and plot PC1 vs PC2.

A remarkable thing happens: each "family" forms a triplet of points that are all close together. Of course every child is closer to each of its parents in the original 10,000-dimensional space so one could expect it to be close to the parents also in the PCA space. However, in the PCA space each pair of parents is close together as well, even though in the original space they are just random points!

How do children manage to pull parents together in the PCA projection?

$\quad\quad\quad\quad$

One might worry that this is somehow influenced by the fact that the children have lower norm than the parents. This does not seem to matter: if I produce the children as $(x+y)/\sqrt{2}$ where $x$ and $y$ are parental points, then they will have on average the same norm as the parents. But I still observe qualitatively the same phenomenon in the PCA space:

$\quad\quad\quad\quad$

This question is using a toy data set but it is motivated by what I observed in a real-world data set from a genome-wide association study (GWAS) where dimensions are single-nucleotide polymorphisms (SNP). This data set contained mother-father-child trios.

---

Code

%matplotlib notebook

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)

def generate_families(n = 10, p = 10000, divide_by = 2):
    X1 = np.random.randn(n,p)    # mothers
    X2 = np.random.randn(n,p)    # fathers
    X3 = (X1+X2)/divide_by       # children
    X = []
    for i in range(X1.shape[0]):
        X.extend((X1[i], X2[i], X3[i]))
    X = np.array(X)

    X = X - np.mean(X, axis=0)
    U,s,V = np.linalg.svd(X, full_matrices=False)
    X = U @ np.diag(s)
    return X

n = 10
plt.figure(figsize=(4,4))
X = generate_families(n, divide_by = 2)
for i in range(n):
    plt.scatter(X[i*3:(i+1)*3,0], X[i*3:(i+1)*3,1])
plt.tight_layout()
plt.savefig('families1.png')

plt.figure(figsize=(4,4))
X = generate_families(n, divide_by = np.sqrt(2))
for i in range(n):
    plt.scatter(X[i*3:(i+1)*3,0], X[i*3:(i+1)*3,1])
plt.tight_layout()
plt.savefig('families2.png')

Answer 1

During the discussion with @ttnphns in the comments above, I realized that the same phenomenon can be observed with many fewer than 10 families. Three families (n=3 in my code snippet) appear roughly in the corners of an equilateral triangle. In fact, it is enough to consider only two families (n=2): they end up separated along PC1, with each family projected roughly onto one point.

The case of two families can be visualized directly. The original four points in the 10,000-dimensional space are nearly orthogonal and reside in a 4-dimensional subspace. So they form a 4-simplex. After centering, they will form a regular tetrahedron which is a shape in 3D. Here is how it looks like:

Before the children are added, PC1 can point anywhere; there is no preferred direction. However, after two children are positioned in the centers of two opposite edges, PC1 will go right through them! This arrangement of six points was described by @ttnphns as a "dumbbell":

such a cloud, like a dumbbell, will tend to pull the main PCs so that these pierce the heavy regions

Note that the opposite edges of a regular tetrahedron are orthogonal to each other and are also orthogonal to the line connecting their centers. This means that each family will be projected to one single point on PC1.

Perhaps even less intuitively, if the two children are scaled by the $\sqrt{2}$ factor to give them the same norm as the parents have, then they will "stick out" of the tetrahedron, resulting in PC1 projection with both parents collapsed together and child being further apart. This can be seen in the second figure in my question: each family has its parents really close on the PC1/PC2 plane (EVEN THOUGH THEY ARE UNRELATED!), and their child is a bit further apart.