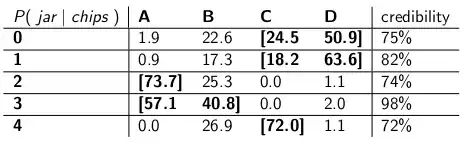
I am looking on expanding my introductory knowledge in stat, and I have come up with this challenge. I have an application that is designed to analyze and index news articles. The goal of the application is to count the number of occurrences of a certain word, and to show how many times this count occurs in a dataset. In a following bar chart, I have made one such analysis.
As I said, from the chart it is visible that there are 942 examples of a words that repeat only once. However, there is only 1 example of a word that is repeated 160 times.
So, my question is how can I, with a certain degree of probability, confirm that my word distribution is following a theoretically defined distribution? In order to answer to this question, I have used R's
fitdistrplus library
to plot a Cullen - Frey graph that could point me in the right direction of choosing a probable distribution. The code in R, to plot my y-axis values looks like this:
library(fitdistrplus)
library(logspline)
x <- c(942, 125, 54, 28, 10, 6, 11, 5, 9, 1, 5, 3, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1,1)
descdist(x, discrete = TRUE, boot = 500)
This produces a following chart:
From the chart it can be deduced that the data is suggesting to be in the negative binomial distribution area. However, I am not sure how to confirm my claim with greater level of confidence, and I would like an opinion on the process done so far?
Revised data
After a comment by a fellow colleague, I have revised my data that is being import into R's descdist() function. The newly formulated data now accounts for the zero values that are obviously part of my count-data set.
The revised R code looks like this:
library(fitdistrplus)
xx <- 0:160
y <- c(0,942,125,54,28,10,6,11,5,0,9,1,5,3,0,0,1,2,0,0,1,0,0,0,2,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1)
obs <- rep(xx,y)
# plot the histogram
hist(obs, freq=TRUE, breaks=1000)
# Describe with Cullen & Frey Graph
descdist(obs, discrete = TRUE, boot = 500)
It produces the following CF graph:
What I think is critical, and I have changed it in this revised addition is that now I am modeling with 2D data set, in which both of my X and Y axises are present.
What I would still like to find out, how to confirm my suspicion that the distribution is Negative Binomial? And if my R code valid now?
P.S. I have even fitted the distributions NB and Poisson distribution to get AIC score, which is the following:
fit.nbinom <- fitdist(obs, "nbinom")
fit.pois <- fitdist(obs, "pois")
plot(fit.nbinom)
summary(fit.nbinom)
fit.nbinom$aic
plot(fit.pois)
summary(fit.pois)
fit.pois$aic
1 4707.648 (AIC for NB)
2 7378.281 (AIC for Poisson)