Comment (continued): As a particular example using R, let
$X_1 \sim \mathsf{Norm}(\mu = 1, \sigma = 1),$
$X_2 \sim \mathsf{Norm}(\mu = 2, \sigma = 1),$ and
$X_3 \sim \mathsf{Norm}(\mu = 3, \sigma = 1).$
Then $Q = \sum_{i=1}^3 X_i^2\sim \mathsf{Chisq}(\nu = 3, \lambda=14).$
Demonstration using simulation:
set.seed(1108); m = 10^6
mu = c(1,2,3) # mean vector recycles
x = rnorm(m*3, mu, 1)
MAT = matrix(x, nrow=m, byrow=T) # m x 3 matrix
q = rowSums(MAT^2)
mean(q)
[1] 17.00669 # aprx df + ncp = 17
hist(q, prob=T, col="skyblue2", main="Simulated CHISQ(df=3,ncp=14)")
curve(dchisq(x, 3, ncp=14), add=T, lwd=2, col="red")
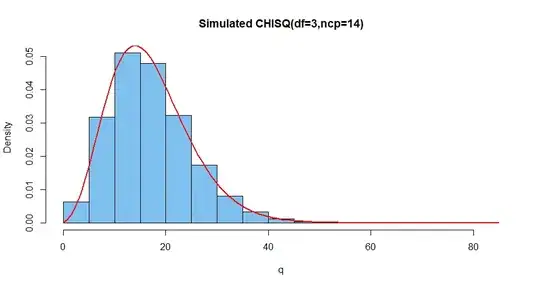
See R documentation of dchisq for details of the R function and
Wikipedia for
the PDF and moments of the non-central chi-squared distribution. I will leave
it to you to handle the constant multiple in case the normal distributions
have the same variance $\sigma^2.$ [If the normal distributions have different variances, then it may be best to think in terms of $\sum_i \frac{(X_i-\mu_i)^2}{\sigma_i} \sim \mathsf{Chisq(n)}.]$
