1

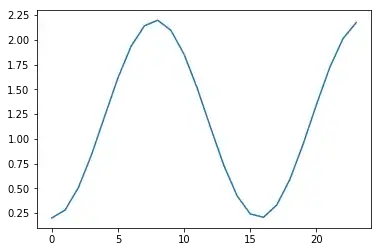
I have generated 100 sample time series, each 24 items long, and each with an exponential distribution with a different scale for each of the 24 time points. This is the scale parameter per time point:

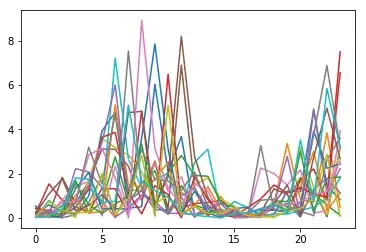
enter image description here

My 100 time series look like this:

enter image description here

This is the sample covariance matrix:

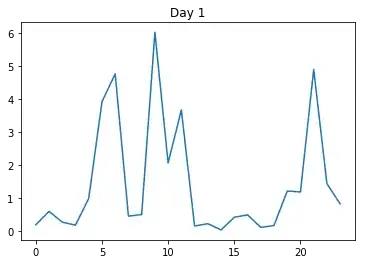
enter image description here

Now this is the first day:

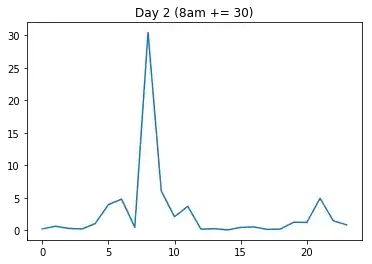
enter image description here

Now I will artificially create two new days: One where I add a lot to one time point where the variance is generally high (day2 gets an increase at 8 o'clock), and another one where I add the same amount to a time point where the variance is low (day3 gets the same increase at 2am).

I will expect that the distance dist(day1, day2) is a lot smaller than dist(day1, day3), because day2's increase happened in a high-variance region (8am, that is).

enter image description here enter image description here

But the output I get is:

mahalanobis(day1, day2, Sigma)  # should be "small"
62.9029

mahalanobis(day1, day3, Sigma)  # should be larger
15.0200

Why is the distance dist(day1, day2) larger than dist(day1, day3)?

Edit: Python code to reproduce the figures and results:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

one_day_length = 24
n_days = 400

x = np.array(range(one_day_length))
scales = 0.2 + 2 * np.sin(x / 5) ** 2

# plt.plot(scales)

np.random.seed(20181106)
one_random_day = np.random.exponential(scale=scales, size=one_day_length)

# plt.plot(one_random_day)

random_days = pd.DataFrame([np.random.exponential(scale=scales, size=one_day_length) for _ in range(n_days)])

# random_days.head(20).T.plot(legend=False)

Sigma = random_days.cov()

from scipy.spatial.distance import mahalanobis

day1 = random_days.iloc[0]

# plt.plot(day1)
# plt.title('Day 1')

# plt.imshow(Sigma)

mahalanobis(day1, day1, Sigma)  # 0 of course

day2 = day1.copy()
day2[9] += 30
# plt.plot(day2)
# plt.title('Day 2 (8am += 30)')

day3 = day1.copy()
day3[2] += 30
# plt.plot(day3)
# plt.title('Day 3 (2am += 30)')

mahalanobis(day1, day2, Sigma)  # should be "small", but is 64.61
mahalanobis(day1, day3, Sigma)  # should be larger, but is 15.02
Alexander Engelhardt
  • 4,161
  • 3
  • 21
  • 25
  • 2
    Your intuition is the opposite of how Mahalanobis distance works. See https://stats.stackexchange.com/questions/62092 for explanations. Note that this generalizes the basic concept of "standardization" or "z scores" from one dimension to many. Specifically, adding a large amount to a variable that has a large variance will scarcely change its z score, while adding the same amount to a variable with small variance will make a large change in its z score. – whuber Nov 07 '18 at 14:42
  • 1
    Thanks! But your explanation is exactly my intuition, as far as I understand. Your last sentence is exactly what I expected here - and what didn't happen. In the "Day 2" plot, I add a large amount (30) to a variable (x=8am) that has large variance (see 2nd and 3rd image). That should scarcely change the z-score, i.e. result in a small distance of mahalanobis(day1, day2), relative to mahalanobis(day1, day3), right? – Alexander Engelhardt Nov 07 '18 at 15:19
  • 1
    Nope--you have it exactly backwards. Adding $30$ to a variable with a variance of, say, $100^2$ adds $0.3$ to its z score. Adding 30 to a variable with a variance of $10^2$ adds $3$ to its z score. The latter is a much greater change. – whuber Nov 07 '18 at 15:30
  • 1
    I am confused :/ In my opinion you and I are saying the same thing. I understand that adding $30$ to a variable with a variance of $100^2$ is a smaller change than adding $30$ to a variable with variance $10^2$. That's exactly what I did in my plots (right?). Now I'm confused why the distance d(day1, day2) is larger than d(day1, day3), even though I added to the high-variance variable in day2, and I added to the low-variance variable in day3. I expected day3 to be more "extreme" (like you just explained above). – Alexander Engelhardt Nov 08 '18 at 07:18
  • Could you add a reproducible example, i.e., code generating the data, adding 30, computing the distances? What is the distance between day1 and unmodified day2 vs. the distance between day1 and unmodified day3? – Juho Kokkala Nov 08 '18 at 19:43
  • @JuhoKokkala I've added Python code at the end that reproduces the results and figures in this question. The distance between unmodified day2 and day1 is zero (I just copied the array). – Alexander Engelhardt Nov 09 '18 at 16:23

1 Answers1

4

The strange result is due to a programming error - according to https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.spatial.distance.mahalanobis.html the mahalanobis-function in question takes inverse covariance matrix as input. Fixing the code as, e.g., 

invSigma = np.linalg.inv(Sigma.values)
mahalanobis(day1, day2, invSigma)  # 14.41
mahalanobis(day1, day3, invSigma)  # 61.93

produces results matching with the expectation.

Indeed, since we are here adding $\Delta=30$ to $j$th element of the vector (day1), keeping the other elements constant, the Mahalanobis distance simplifies as \begin{equation} \sqrt{(\mathbf{x}+\Delta\mathbf{e}_j-\mathbf{x})^T\,V^{-1}\,(\mathbf{x}+\Delta\mathbf{e}_j-\mathbf{x})} = |\Delta|\,\sqrt{(V^{-1})_{j,j}}. \end{equation}

In the setting of the question, the covariance matrix is pretty close to diagonal since it's a sample covariance of data produced from a distribution where the components are independent, and thus $(V^{-1})_{j,j}$ is close to $V_{j,j}^{-1}$. Hence, OP's expectation that modifying a component with high variance should produce a smaller Mahalanobis distance is correct. In presence of correlation, the diagonal element of $(V^{-1})$ measures the residual variance controlling for the other variables (https://stats.stackexchange.com/a/73499/24669). That is to say, the order of the distances could have been different if the high-variance point 8 am was highly correlated with other components.

Juho Kokkala
  • 7,463
  • 4
  • 27
  • 46