The title pretty much says it all. I have data that consists of 80 samples but there are always at least four samples that have exactly the same value. I want to assess, whether the data is unimodal. Now the plot of the kernel density estimate shows clearly that the data has two "hooks":
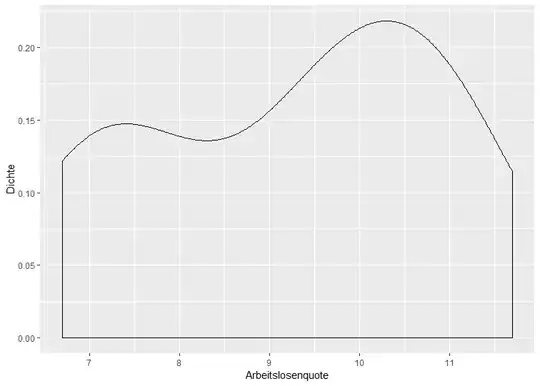 However this data would have never been obtained by any continuous probability distribution, so I am not sure whether it is appropriate to use a kernel density estimate at all?
However this data would have never been obtained by any continuous probability distribution, so I am not sure whether it is appropriate to use a kernel density estimate at all?