How to convert the parameters in a binomial distribution to those in a beta distribution?

Question

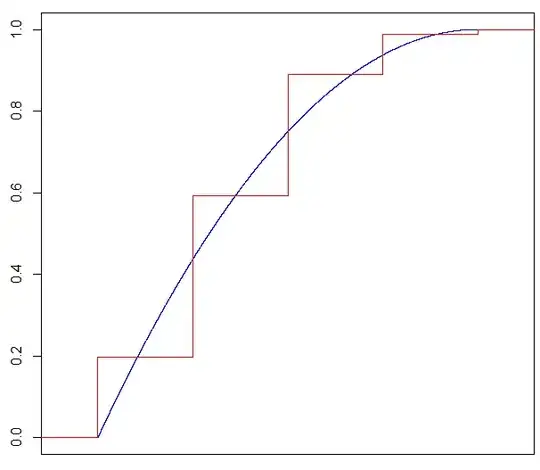
I know that the beta distribution is the generalized continuous case of the discrete binomial distribution. Let's say I have a binomial distribution, $B(N,p)$. I would like to know the corresponding $\alpha$ and $\beta$ such that the binomial CDF of any count, $k$, in $\{0,1,2,...,N\}$ equals to the beta CDF at $x = k/N$.

In terms of equations, I would like the functions $f(x)$ and $g(x)$ such that:

1. $\alpha = f(N,p)$ and $\beta = g(N,p)$, and
2. CDF of $B(k,n,p) = $ CDF of $Beta(k/N, \alpha, \beta)$ where
   • $N$ in $\mathbb{N}$,
   • $p$ in $(0,1)$, and
   • $k$ in $\{0,1,2,...,N\}$

I have been in search for a while but I find no direct answer. I don't have much maths background and I am hoping for an easy answer in terms of $f(x)$ and $g(x)$.

Answer 1

I do not know that the beta distribution is the generalized continuous case of the discrete binomial distribution, and I am curious why you think that. $p^x(1-p)^{n-x}$ is not really the same as $x^{\alpha-1}(1-x)^{\beta-1}$. What I do know is that the beta distribution provides a conjugate family for the parameter $p$ of the binomial distribution, but that is a rather different statement

You have a problem in that the cumulative distribution functions are not going to match like that. For example, for $X$ binomial you have $P(X\le 0)=\frac{1}{(1-p)^n}$ while for $Y$ beta-distributed you have $P\left(Y \le \frac0n\right) =0$

So if you want an approximate match between the two distributions, an alternative could be to match the means and variances. That could suggest using something like $\alpha=(n-1)p, \beta=(n-1)(1-p)$ or in the other direction $n=\alpha+\beta+1, p= \frac{\alpha}{\alpha+\beta}$

For example with $n=4, p=\frac13$ this might suggest $\alpha=1, \beta=2$, and the following chart is what the two cumulative distribution functions would look like; the relationship is not bad, but you would not use one to calculate the other

Answer 2

The simplest relationship between beta and binomial distributions is

cdf_binomial(N,i,p) = sf_beta(p,i+1,N-i) (where sf_beta, the survival function is 1-cdf_beta)

or equivalently, cdf_binomial(N,i,p) = cdf_beta(1-p,N-i,i+1)

where i >= 0 and i < N