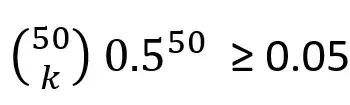0

For a weekly jury duty there are 50 places for men, and women. The probability of choosing a man, or a woman is equal to 0.5.

Given that:

  1. The number of men for a random week is a binomial distribution.
  2. H0: The number of men in a jury duty is completely random

  3. We have a significance level of 0.05.

    We wish to know for which number of men (k), the H0 is passed?

My answer is:

We have to find k in a way that it satisfy the below statement:

enter image description here

But, i don't know how to obtain the K?

In other words, i am not sure, how many valid Ks can pass H0?

Jimmy
  • 127
  • 6
  • Could you articulate the reasons for the "below statement"? By doing so, you might discover what is incorrect about it. See https://stats.stackexchange.com/questions/31 for more about this. – whuber Nov 04 '18 at 15:46
  • For $ k = 21,22,...,29$, $\binom{50}{k} 0.5^{50} > 0.05$ – user158565 Nov 04 '18 at 21:23
  • @a_statistician: True: in R `k = 0:50; pdf = choose(50,k)*.5^50; k[pdf > .05]` returns `21 22 23 24 25 26 27 28 29`. But how is that relevant? – BruceET Nov 04 '18 at 23:31
  • His question is how many valid Ks. So answer is 9. – user158565 Nov 04 '18 at 23:42
  • @a_statistician: But not directly relevant to testing the hypothesis at hand. See whuber's Comment. – BruceET Nov 05 '18 at 01:15
  • No (to 9 'valid' k's). Values of $k$ that do not lead to rejection are between 18 and 32. The rejection region is $k \le 17$ or $k \ge 33.$ (So 15 values don't lead to rejection.) // I was agreeing that values 21 through 29 do all have probabilities exceeding 0.05, but _not_ that this is a correct way to test $H_0: p = 1/2.$ – BruceET Nov 05 '18 at 08:23

1 Answers1

0

Here is a graphical clue.

The plot below shows the PDF of the distribution $\mathsf{Binom}(n = 50,\, p=.5).$ This describes probabilities for various numbers of men in the jury pool if men and women are equally likely to be chosen.

I claim that heights of the vertical orange lines for the numbers of men 0 through 17 and 33 through 50 sum to just less than 0.05. (Including 18 and 32 would put the sum above 0.05.) I will leave it to you to verify this by methods appropriate to your course.

enter image description here

So, at the 5% significance level, it would not be surprising to see anywhere between 18 and 32 men in the jury pool. I will leave it to you to explain the logic of this.

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • Thanks for the answer, i just edited your answer, and added your `R` code to it. it was very useful. – Jimmy Nov 05 '18 at 04:32
  • The values indicating significant differences from 50% are in orange on the graph. These are established in terms of the binomial CDF, not PDF. The total probability of the orange outcomes 0 through 17 is less than 2.5%; similarly for values 33 to 50 (another 2.5% in the right tail). – BruceET Nov 05 '18 at 08:13
  • just out of curiosity, did u reject the my edit? – Jimmy Nov 05 '18 at 08:30
  • Yes, for reason now explained in comments directly below the Question. (I was disagreeing with a_statistician's answer, not his/her computation.) The R code there is not relevant to testing whether the jury pool tends to choose half men and half women. `sum(dbinom(0:17, 50, .5))` returns 0.01641957 < .025. Similarly for right tail. [You can't include 18 (or 32) in rejection region `sum(dbinom(0:18, 50, .5))` returns 0.03245432 > .025. – BruceET Nov 05 '18 at 08:40
  • If you use the normal approximation to the binomial, probabilities are not exact. Depending on the method of approximation and the rounding to use printed normal tables, you might be led to reject for 18 and 32. // Usually authors contrive normal approx problems so that normal approx and exact binomial results agree, maybe not so here. – BruceET Nov 06 '18 at 20:22