Is Cauchy distribution somehow an "unpredictable" distribution?

Question

Is Cauchy distribution somehow an "unpredictable" distribution?

I tried doing

cs <- function(n) {
  return(rcauchy(n,0,1))
}

in R for a multitude of n values and noticed that they generate quite unpredictable values occasionally.

Compare that to e.g.

as <- function(n) {
  return(rnorm(n,0,1))
}

which always seems to give a "compact" cloud of points.

By this pic it should look like the normal distribution? Yet it maybe only does for a subset of values. Or maybe the trick is that the Cauchy standard deviations (in the pic below) converge much more slowly (to left and right) and thus is allows for more severe outliers, although at low probabilities?

Here as are normal rvs and cs are Cauchy rvs.

But by the extremity of the outliers, is it possible that the tails of the Cauchy p.d.f. never converge?

Answer 1

While a number of posts on site address various properties of the Cauchy, I didn't manage to locate one that really laid them out together. Hopefully this might be a good place to collect some. I may expand this.

Heavy tails

While the Cauchy is symmetric and roughly bell shaped, somewhat like the normal distribution, it has much heavier tails (and less of a "shoulder"). For example, there's a small but distinct probability that a Cauchy random variable will lay more than 1000 interquartile ranges from the median -- roughly of the same order as a normal random variable being at least 2.67 interquartile ranges from its median.

Variance

The variance of the Cauchy is infinite.

Edit: J.G. says in comments that it's undefined. If we take the variance as the average of half the squared distance between pairs of values - which is identical to the variance when both exist, then it would be infinite. However, by the usual definition J.G. is correct. [Nevertheless by contrast with sample means, which don't really converge to anything as n becomes large, the distribution of sample variances keep growing in size as the sample size increases; the scale increases proportionally to n, or equivalently the distribution of log variance grows linearly with sample size. It seems productive to actually consider that version of variance that yields infinity is telling us something.]

Sample standard deviations exist, of course, but the larger the sample the larger they tend to be (e.g. the median sample standard deviation at n=10 is in the vicinity of 3.67 times the scale parameter (half the IQR), but at n=100 it's about 11.9).

Mean

The Cauchy distribution doesn't even have a finite mean; the integral for the mean doesn't converge. As a result, even the laws of large numbers don't apply -- as n grows, sample means don't converge to some fixed quantity (indeed there's nothing for them to converge to).

In fact, the distribution of the sample mean from a Cauchy distribution is the same as the distribution of a single observation(!). The tail is so heavy that adding more values into the sum makes a really extreme value likely enough as to just compensate for dividing by a larger denominator when taking the mean.

Predictability

You can certainly produce perfectly sensible prediction intervals for observations from a Cauchy distribution; there are simple, fairly efficient estimators that perform well for estimating location and scale and approximate prediction intervals can be constructed -- so in that sense, at least, Cauchy variates are 'predictable'. However, the tail extends very far, so that if you want a high-probability interval, it may be quite wide.

If you're trying to predict the center of the distribution (e.g. in a regression type model), that may in some sense be relatively easy to predict; the Cauchy is quite peaked (there's a lot of the distribution "close" to the center for a typical measure of scale), so the center can be relatively well-estimated if you have an appropriate estimator.

Here's an example:

I generated data from a linear relationship with standard Cauchy errors (100 observations, intercept=3, slope=1.5), and estimated regression lines by three methods that are reasonably robust to y-outliers: Tukey 3 group line (red), Theil regression (dark green) and L1-regression (blue). None are especially efficient at the Cauchy - though they would all make excellent starting points for a more efficient approach.

Nevertheless the three are almost coincident compared to the noisiness of the data and lay very close to the centre of where the data runs; in that sense the Cauchy is clearly "predictable".

The median of the absolute residuals is only a little larger than 1 for any of the lines (most of the data lay quite close to the estimated line); in that sense as well, the Cauchy is "predictable".

For the plot on the left there's a large outlier. In order to see the data better I narrowed the scale on the y-axis down on the right.

Answer 2

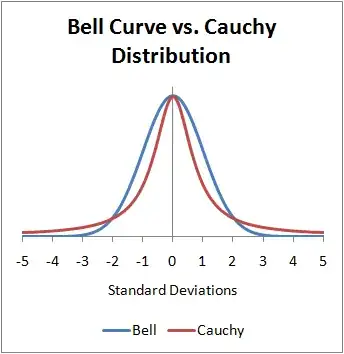
No, the Cauchy distribution is a very predictable distribution in the sense that the fractiles are well defined. If you know $\mu$ and $\sigma$, then the location probability that an observation will appear between any two points, from a sample size where $n\to\infty$ is well defined. However, while 50% of the data will appear in $\mu\pm\sigma$, the central 99.95% of the data will be $\mu\pm{636.62}\sigma$.

In addition, $\sigma$ is not a standard deviation; it is a scale parameter. There is no defined mean, so the higher moments do not exist either. It is often said that the mean and variance are infinite and under one definition of the integral that is almost true, but in another understanding of the integral, they simply do not exist. You may want to think of a variance or a mean as a property that some distributions have, but not others. Just as noses are a property of vertebrates, if you see a tree with a nose, then it is not a tree. If you see a distribution with a variance, then it is not the Cauchy distribution.

The Cauchy distribution appears quite a bit in nature, particularly where you have some form of growth. It also appears where things spin, such as rocks rolling down hills. You will find it as the core distribution of an ugly mixture of distributions in stock market returns, though not in returns for things like antiques sold in auctions. Returns on antiques also belong to a distribution without a mean or a variance, but not a Cauchy distribution. The differences are created by the differences in the rules of the auction. If you changed the rules of the NYSE, then the Cauchy distribution would disappear, and a different one would appear.

To understand why it is usually present, imagine you were a bidder in a very large set of bidders and potential bidders. Because stocks are sold in a double auction, the winner's curse does not apply. In equilibrium, the rational behavior is to bid your expected value. An expectation is a form of the mean. A distribution of mean estimates will converge to normality as the sample size goes to infinity.

So prices, if the firm isn't going to go bankrupt or become bought out in a merger, will be normally distributed if there is no cost for liquidity (which there is). If the quantity of shares do not change, then the return for investing at time t is $$r_t=\frac{p_{t+1}}{p_t}$$. That makes it the ratio of two normal distributions. If the integration happens around the equilibrium prices, rather than at (0,0), you will end up with a truncated Cauchy distribution. If you disaggregate returns into individual transactions over the 20th century, you will find that a truncated Cauchy closely matches the actually observed returns once you remove mergers, liquidity costs, and bankruptcies.

This makes the stock market very volatile, if one thinks that the stock market should have a normal or log-normal distribution, but not unexpectedly volatile if you are expecting the heavy tails.

I have constructed both the Bayesian and the Frequentist predictive distributions for the Cauchy distribution and given their assumptions they work well. The Bayesian prediction minimizes the Kullback-Leibler divergence, meaning it is as close as you can get to nature in a prediction, for a given data set. The Frequentist prediction minimizes the average Kullback-Leibler divergence over many independent predictions from many independent samples. It doesn't necessarily perform well, though, for any one sample as one would expect with average coverage. The tails do converge, but they converge slowly.

The multivariate Cauchy has even more upsetting properties. For example, while it obviously cannot covary since there is no mean, it has nothing similar to a covariance matrix. Cauchy errors are always spherical if nothing else is going on in the system. In addition, while nothing covaries, nothing is independent either. To understand how important that could be in a practical sense, imagine two countries that are both growing and that they trade with each other. The errors in one are not independent of the errors in the other. My mistakes influence your mistakes. If one country is taken over by a madman, the mistakes of that madman are felt everywhere. On the other hand, since the effects are not linear as one would expect with a covariance matrix, the other countries can sever relationships to minimize the impact. North Korea is an example of this.

This is also what makes Trump's trade war so dangerous. The world's second-largest economy after the European Union declared economic war through trade against every other single economy and is financing that war by borrowing the money to fight it from the nations it declared war on. If those dependencies are forced to unwind, it will be ugly in a way that nobody has a living memory of. We hadn't had a similar problem since the Jackson Administration when the Bank of England embargoed the Atlantic trade.

The Cauchy distribution is fascinating because it appears in exponential and S-curve growing systems. They confuse people because their day to day life is filled with densities that do have a mean and usually have a variance. It makes decision making very difficult because the wrong lessons are learned.