Why is the amount of variance explained by my 1st PC so close to the average pairwise correlation?

Question

What is the relationship between the first principal component(s) and the average correlation in the correlation matrix?

For example, in an empirical application I observe that the average correlation is almost the same as the ratio of the variance of the first principal component (first eigenvalue) to the total variance (sum of all eigenvalues).

Is there a mathematical relationship?

Below is the chart of the empirical results. Where correlation is the average correlation between DAX stock index component returns computed over 15-day rolling window and the explained variance is the share of the variance explained by the first principal component, also computed over the 15-day rolling window.

Could this be explained by a common risk factor model such as CAPM?

Answer 1

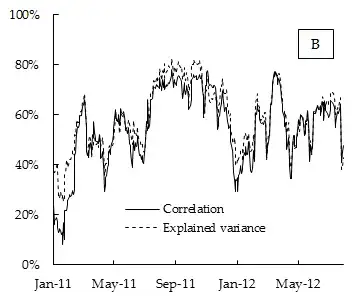
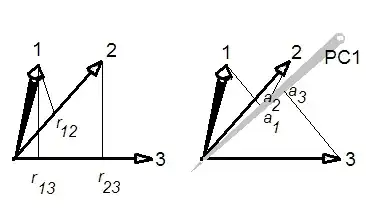
What I think happened here is that all variables were positively correlated with each other. In this case the 1st PC quite often turns out to be very close to the average of all the variables. If all variables are positively correlated with exactly the same correlation coefficient $c$, then the 1st PC is exactly proportional to the average of all the variables, as I explain here: Can averaging all the variables be seen as a crude form of PCA?

In this simple case one can actually mathematically derive the relationship you are asking about. Consider correlation matrix of $n\times n$ size that looks like that: $$\left(\begin{array}{}1&c&c&c\\c&1&c&c\\c&c&1&c\\c&c&c&1\end{array} \right).$$ Its first eigenvector is equal to $(1,1,1,1)^\top/\sqrt{n}$, which corresponds to the [scaled] average of all the variables. Its eigenvalue is $\lambda_1=1+(n-1)c$. The sum of all eigenvalues if of course given by the sum of all diagonal elements, i.e. $\sum \lambda_i=n$. So the proportion of explained variance by the first PC is equal to $$R^2=\frac{1}{n}+\frac{n-1}{n}c \approx c.$$

So in this most simple case the proportion of explained variance by the first PC is 100% correlated with the average correlation, and for large $n$ is approximately equal to it. Which is precisely what we see on your plot.

I expect that for large matrices, this result will approximately hold even if the correlations are not exactly identical.

---

Update. Using the figure posted in the question, one can even try to estimate the $n$ by noticing that $n=(1-c)/(R^2-c)$. If we take $c=0.5$ and $R^2-c=0.02$, then we get $n=25$. The OP said that the data was a "DAX stock index"; googling it, we see that it apparently consists of $30$ variables. Not a bad match.

Answer 2

I believe the relationship between the mean correlation and the eigenvalue of the 1st PC exist but is not unique. I'm not a mathematician to be able to deduce it, but I can at least display the starting point where one's intuition or thought might grow from.

If you draw standardized variables as vectors in euclidean space that seats it (and this is the reduced space where axes are observations), correlation is the cosine between two vectors.

And because vectors are all of unit length (due to standardization) the cosines are the projections of the vectors on each other (like shown on the left picture with three variables). The 1st PC is such a line in this space that maximizes the sum of squared projections onto it, a's, called loadings; and this sum is the 1st eigenvalue.

So, when you establish the relationship between the mean of the three projections on the left with the sum (or mean) of the three squared projections on the right, you answer your question about the relationship between the mean correlation and the eigenvalue.