I have learned some about a simple logistic regression with one explanatory variable (quantitative) and one response variable (binary: $0$ or $1$)
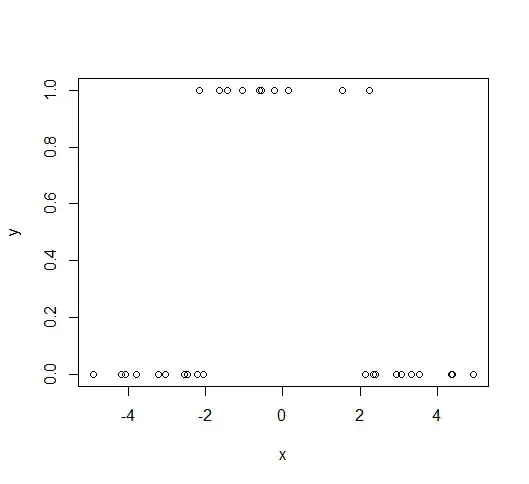
Generally the plot for such a set of data may look like this:
Then we can run a logistic regression to find a model to fit the data.
However, it looks as if in general the rule for the model is, the higher we let our explanatory variable be, the higher the probability that we would have a success.
What if our data suggested otherwise, and instead going too high would end up giving a response variable of $0$ again. Another way to ask my question is, what if our data looks a little something like this:
Would a logistic model even be viable still in this situation? If not, then what kind of nonlinear regression would represent something like this?
Thanks for any clarification given.