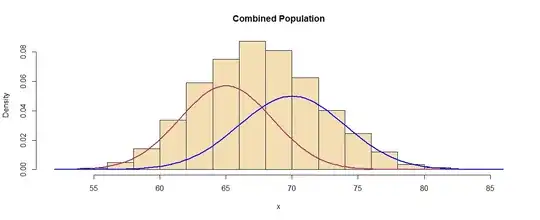
Can someone help me understand this regarding the difference between two means?
Suppose the mean height of US males is 70 inches with a standard deviation of 4 inches and the mean height for US females is 65 inches with a standard deviation of 3.5 inches. Running a t-test of the difference of means will be significant, even assuming small sample size. But if you plot a normal distribution of each of the two, there is significant overlap. For males, two standard deviations below reaches to 62 inches, well past the female mean. Likewise, for females, two standard deviations below reaches to 72 inches. So how are these considered statistically different? Here is a website depicting the two normal curves: http://www-users.math.umn.edu/~johngoes/stats.html
I feel my inability to understand this is hindering my ability to understand statistics entirely.
I think maybe it relates to sampling distributions somehow, which will have a smaller standard error, which is being estimated from the standard deviation of the population.
Can someone help an idiot like me understand this?