Which features would you extract out of these time series?

Question

I have around 2000 time series, each of around 40 values. In the image you see a random selection of 4 of those 2000 time series with a smoothed line in orange.

I would like to calculate around 3 to 5 good features for each time series. Of course you can calculate the mean and the max and other straightforward statistics, but I hope the features also describe characteristics like:

• The trend today, 10 years ago, 20 years ago?
• Did the timeseries have already have maximum?

Which method would you use?

Answer 1

I ended building an auto encoder, which is a neural network with the following structure.

The input are the values of each timeseries, the output the same values. So this neural network tries to reconstruct the timeseries after passing through a hidden layer with only a couple of neurons (the autoencoder I build had only three neurons in the middle hidden layer).

Training this neural network is really simple with Keras / Tensorflow (you can find some inspiration here: https://blog.keras.io/building-autoencoders-in-keras.html). When the neural network is trained, you simple pass through all the timeseries and record the values of the hidden neurons for each timeseries. This is your feature matrix!

To illustrate that this works really well, take a look at the following image. For a couple of timeseries (the occurrence of a given name in the Netherlands for each year), I used these the features to find names with a similar timeseries. You see that it effectively selects similar names, although it did not use the full timeseries (42 values) but only the 3 features.

Answer 2

I think what is described can be a very convenient application of Functional Principal Component Analysis.

In short: through FPCA we will be able to find the major axes of variation in our longitudinal sample $Y$, those axes would be the FPCs ($\phi$) themselves. The $\phi$'s can serve as our interpretable time-series features' we will be able to plot them, discuss them, quantify how much variation they encapsulate as well as directly employ them onto another sample. Some simplistically we will do covariance-derived PCA on our sample and get the eigenfunctions $\phi$ as our features.

In a bit more detail: The FPC scores ($\xi_{ij}$) associated will each FPC $\phi_j$ will give us a direct measurement of how much each FPCs $\phi_j$ is "used" in the construction of the original time-series $y_i$. Through FPCA we will be guaranteed to have the optimal representation (in terms of $L_2$ norm) for a given number of feature/FPCs $k$ if we use a linear basis. This is because we will effectively do a PCA analysis using the (auto-)covariance matrix $C$ of the process that defines our sample $Y$. (i.e. we will get the spectral decomposition of $C$ such that $C(t,t') = \sum_{k=1}^\infty \lambda_k \phi_k(t) \phi_k(t')$). The eigenvalues $\lambda_k$ allow us to directly determine the total percentage of sample variation exhibited along the $k$-th FPC and can help us determine how many components to use (i.e. they guard us from questions like: "Why $n$ features, and not $n+2$ or $n-1$ features?" ); thus the choice of the number of features (FPCs) can be directly tied to a fraction-of-variance-explained criterion (e.g. 80%, 90%, etc.).

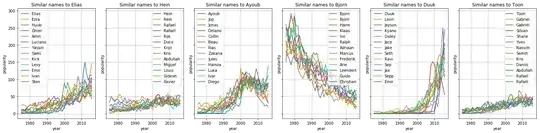
The literature of applying FPCA to time-series is pretty vast (e.g. Shang & Hyndman (2011) Nonparametric time series forecasting with dynamic updating, Ingrassia & Costanzo (2005) Functional Principal Component Analysis of Financial Time Series, Bouveyron & Jacques (2011) Model-based clustering of time series in group-specific functional subspaces, etc.); I would suggest looking at a standard handbook like Horvath and Kokoszka's Inference for Functional Data with Applications to get some idea; applying FPCA is quite easy. Particular to your case, I actually even found a R package (fdadensity), where they use baby names popularity in their examples. That work actually treats the "popularity" readings as densities, so it has a different perspective than looking at them as standard time-series; the accompanying methodological Annals of Statistics paper by Petersen & Mueller (2016) Functional Data Analysis for Density Functions by Transformation to a Hilbert space is not for the faint of heart...

Note: A PCA-based approach will not guarantee that we get the optimal reconstruction if we allow for non-linear dimensionality reduction techniques. That's why we can get an auto-encoder (AE) that provides better reconstructions than PCA; see the CV thread Building an autoencoder in Tensorflow to surpass PCA for some example on this). Your original idea about using an AE is great. An FPCA approach will probably be easier to justify methodologically (if you need that) as well as show-case what the features are (which is pretty important to get buy-in in certain cases). FPCA should be faster too (the main computational burden is to smooth the covariance matrix (if that is even required).