Christian H Weiss says that:
In general, it is not clear if the ML estimators (uniquely) exist and if they are consistent.
Can someone explain what he means? Do we not generally know the shape of a log-likelihood function once we specify the probability distribution?
A multimodal likelihood function can have two modes of exactly the same value. In this case, the MLE may not be unique as there may two possible estimators that can be constructed by using the equation $\partial l(\theta; x) /\partial \theta = 0$.
Example of such a likelihood from Wikipedia:
Here, see that there's no unique value of $\theta$ that maximises the likelihood. The Wikipedia link also gives some conditions on the existence of unique and consistent MLEs although, I believe there are more (a more comprehensive literature search would guide you well).
Edit: This link about MLEs, which I believe are lecture notes from Cambridge, lists a few more regularity conditions for the MLE to exist.
You can find examples of inconsistent ML estimators in this CV question.
One example arises from rank deficiency. Suppose that you're conducting an OLS regression but your design matrix is not full rank. In this case, there are any number of solutions which obtain the maximum likelihood value. This problem isn't unique to OLS regression, but OLS regression is a simple enough example.
Another case arises in the MLE for binary logistic regression. Suppose that the regression exhibits separation; in this case, the likelihood does not have a well-defined maximum, in the sense that arbitrarily large coefficients monotonically increase the likelihood.
In both cases, common regularization methods like ridge penalties can resolve the problem.
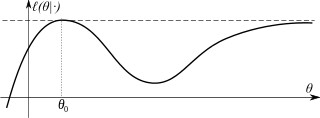
One additional example of non-uniqueness of MLE estimator:
To estimate the location parameter $\mu$ of the Laplace distribution through ML, you need a value $\hat{\mu}$ such that: $$ \sum_{i=1}^n \frac{|x_i - \hat{\mu}|}{x_i - \hat{\mu}} = 0$$
That is, an estimate $\hat{\mu}$ such that the number of observations below and above $\hat{\mu}$ are equal.
Clearly for an even $n > 1$ the solution will not be unique, unless the the two central observations (in ascending order) are the same.
For the sake of simplicity, usually we choose as estimate $\hat{\mu} = \overset{\sim}{x}$ (sample median), because it satisfies the required condition and is a well known statistic, but it might not be the unique answer.
This is troublesome when you're using numerical algorithms that might not converge because there's not a single answer.
Another simple example that shows that the ML Estimator is not always unique is the model $U(\theta, \theta +1)^n$. If your sample is $(x_1, ..., x_n)$ the likelihood $f(x_1,...x_n|\theta)$ for this sample is 1 if $x_i \in [\theta, \theta +1] \forall i=1...n$ and $0$ otherwise.
