I am a computational biologist with little experience fitting data.
I'm trying to fit a distribution of cosine similarities computed between sparse matrices. The goal is to be able use this distribution as a null distribution to compute p-values of computed cosine similarities on real data.
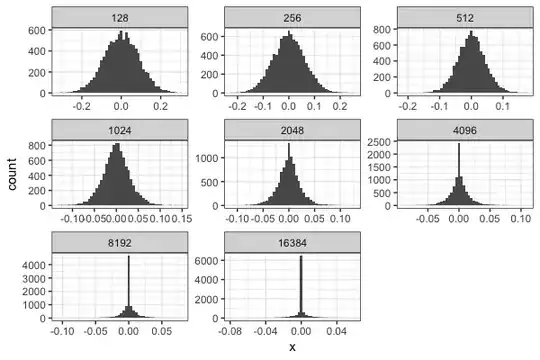
The null distribution of cosine similarities is typically assumed to follow a normal distribution because of the central limit theorem and indeed this is what we see when the vectors are dense.
However, in a biological setting we would more often deal with fairly sparse vectors (~95% 0’s) (in this case we're talking about gene membership to a geneset when the universe of genes increases). When we increase the sparsity of the vectors and plot the distribution of cosine similarities, we see that it rapidly becomes non-normal and inflated at 0. In our simulations, we keep the amount of non zero genes fixed and increase the total size of the vector (with the remaining genes being all 0)
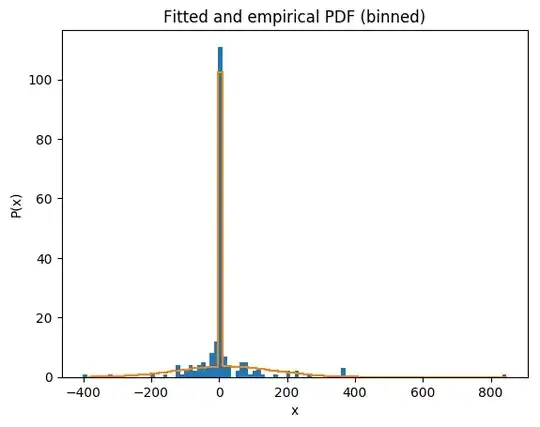
Visually, it looks like the distribution moves from being gaussian to Laplace as sparsity increases. We've tried to fit this dataset using a double exponential (dlaplace from the package jmuOutlier) and the ideas from this post
x <- seq( min(mydata), max(mydata), length.out=20 )
mean_estimated <- median(mydata)
sd_estimated <- mean(abs(mydata-mean_estimated))
laplace_curve <- dlaplace(x, mean=mean_estimated, sd=sd_estimated )
res <- hist(mydata, breaks = 100)
plot(res$mids, res$counts)
hist(mydata, breaks = 100, freq = F)
curve(dlaplace(x, mean=mean_estimated, sd=sd_estimated ), col = "red", add = TRUE)
and here's some sample data
my data <- c(0,0,0,-121.812475497063,-17.1317497626788,0,0,0,8.35572739928506,0,-26.9359145415957,20.4527916510325,0,-4.74715944618195,117.542381259887,232.123630295157,123.223331644106,0,363.307449720702,0,17.2876056009945,48.4743173227965,0,-59.3313238079675,72.1418015633871,26.6828781262261,0,-9.59200428642452,0,0,0,0,0,0,14.7726016702487,0,-325.332919994427,104.648601779681,-41.5876513726268,0,23.8977917597686,0,-4.61753733424316,0,-126.668971720393,1.45200133967801,0,-401.095618197396,16.7718497697131,0,0,361.956158574512,-0.041911914563271,0,0,-154.903446590557,-24.5034756181517,0,-46.4799574666324,0,-78.0146685968426,0,0,0,-12.7363529440765,0.801785045212923,79.7353310556848,263.50396219768,68.7207464247363,-16.6983607980076,0,0,0,0,9.49049366986621,0,-25.2709579790211,18.9158672257186,-16.5083502102244,-123.816047852029,0,10.074510523382,-1.7805270018387,-1.12260723072776,-34.5358930060155,112.65174921281,0,0,0,0,0,0,110.661061532395,-4.76648158660036,0,0,0,64.7388429927619,0,83.4665923262401,-90.5948140823812,48.1520353229011,83.2419061957572,84.6904132512109,-32.5771834489668,0,-24.4646160022276,0,0,16.283865284046,845.919876029546,0,0,30.9790913857609,-64.1857905888979,-71.8981992333845,0,0,-82.3833048984224,0,6.91280012973377,0,14.3260581532408,0,-88.4583037875095,4.81561616305259,0,0,0,0,224.936048456396,2.76354047838483,0,-12.3129795553901,0,0,202.221902345161,3.87903891367971,-6.78101669022923,0,-110.337466635902,0,0,-200.683877785148,0,-52.9434473377721,0,0,0,0,-55.5823775087446,204.412102111891,-89.7181809211675,160.514222115252,-43.1977265125341,-119.720898068799,360.198526060316,0,0,-73.5877173033978,0,0,0,0,0,85.2054592768861,63.8154881905621,-2.45087824145073,0,0,0,0,-36.787934899427,0,0,0,-49.62704298923,-12.549272621154,109.89567398325,0,-19.5206671407738,0,-84.0358460651716,-8.96146044988531,0,0,-40.9156265799148,0,0,88.0444551252554,0,0,23.6917582249244,-11.7178035932228,0,-2.54341767902909,0,63.3618229985467,0,0)
However, there's clearly an inflation in zero that we are not able to fit. Is there a better function suited to fit this type of distribution? Thanks in advance.