Check if a character string is not random

Question

Background
Let's say we have an alphabet of A,B, C, D, then we look through some data and find a "word" which is DDDDDDDDCDDDDDD the chance of finding this random seems low to me whereas finding BABDCABCDACDBACD seems less random.

Question
How should I check whether the strings I encounter are not random?

I tried some things in R, e.g., encoding the letters numerically and then comparing these to permutations. But encoding beforehand is quite cumbersome. Likely there is a more direct approach for this?

Answer 1

the chance of finding this random seems low to me whereas finding BABDCABCDACDBACD seems less random.

Why would that be? If the overall proportion of letters A...D is equal to 0.25 for each letter, and each letter is independent of the other one, then both words are exactly equally probable. If the distribution of letters differ, then of course the probabilities of generating both words might be different.

You can try to find "low complexity" words, for example words with an especially high proportion of one letter (you could use the Shannon information as suggested in the other response, and in biological sequence analysis there are many other approaches), but there is no test for "randomness", as without further assumptions or knowledge about what you are actually analyzing, the term "randomness" makes no sense.

Answer 2

You could try Shannon information: $$ H = -\sum_{i = 0}^n {P_{i}\log_{2}(P_{i})} $$ where, $P_{i} = \frac{c_{i}}{n}$, $c_{i}$ is the count of some letter $c$ in the word and $n = |{\rm word}|$.

For the first word you have $H = 0.35$. In the second word you have $H = 2$.

If the entropy is high, you could think of it as more random vs. another word with lower entropy.

Answer 3

Other answers here have focused on the overall occurrence of different letters in the sequence, which may be one aspect of the "randomness" expected. However, another aspect of interest is the apparent randomness in the order of the letters in the sequence. At minimum, I would think that "randomness" entails the exchangeability of the vector of letters, which can be tested using a "runs test". The runs test counts the number of "runs" in the sequence and compares the total number of runs to its null distribution under the null hypothesis of exchangeability, for a vector with the same letters. The exact definition of what constitutes a "run" depends on the particular test (see e.g., a similar answer here), but in this case, with nominal categories, the natural definition is to count any consecutive sequence consisting of only one letter as a single "run".

For example, your sequence BABD-CABC-DACD-BACD looks prima facie non-random to me (no letter appears with itself, which is probably unusual for a sequence this long).$^\dagger$ To test this formally, we can perform a runs test for exchangeability. In this sequence we have $n = 16$ letters (four of each letter) and there are $r = 16$ runs, each consisting of one single instance of a letter. The observed number of runs can be compared to its null distribution under the hypothesis of exchangeability. We can do this via simulation, which yields a simulated null distribution and a p-value for the test. The result for this sequence of characters is shown in the graph below.

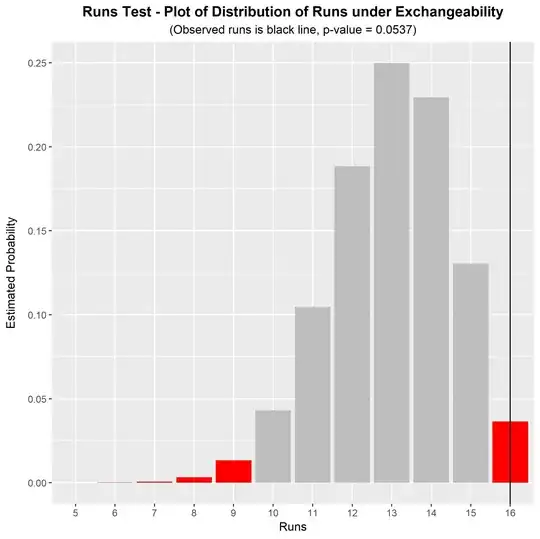
For this sequence, the p-value for the runs test (under the null hypothesis of exchangeability) is $p=0.0537$. This is significant at the 10% significance level, but not at the 5% significance level. There is some evidence to suggest a non-exchangeable series (i.e., non-random order), but the evidence is not particularly strong. With a longer observed string, the runs test would have greater power to distinguish an exchangeable string from a non-exchangeable string. (As you can see, my initial prima facie judgment that this string is non-random may be wrong - the p-value is not actually as low as I expected it to be.)

Finally, it is important to note that this test only looks at the randomness of the order of the letters in the string - it takes the number of letters of each type as a fixed input. This test will detect non-randomness in the sense of non-exchangeability of the letters in the string, but it will not test "randomness" in the sense of overall probabilities of different letters. If the latter is also part of the specified meaning of "randomness" then this runs test could be augmented with another test that looks at the overall counts of the letters, and compares this to a hypothesised null distribution.

---

R code: The above plot and p-value was generated using the following R code:

#Define the character string vector (as factors)
x <- factor(c(2,1,2,4, 3,1,2,3, 4,1,3,4, 2,1,3,4), 
            labels = c('A', 'B', 'C', 'D'))

#Define a function to calculate the runs for an input vector
RUNS <- function(x) { n <- length(x);
                      R <- 1;
                      for (i in 2:n) { R <- R + (x[i] != x[i-1]) }
                      R; }

#Simulate the runs statistic for k permutations
k <- 10^5;
set.seed(12345);
RR <- rep(0, k);
for (i in 1:k) { x_perm <- sample(x, length(x), replace = FALSE);
                 RR[i] <- RUNS(x_perm); }

#Generate the frequency table for the simulated runs
FREQS <- as.data.frame(table(RR));

#Calculate the p-value of the runs test
R      <- RUNS(x);
R_FREQ <- FREQS$Freq[match(R, FREQS$RR)];
p      <- sum(FREQS$Freq*(FREQS$Freq <= R_FREQ))/k;

#Plot estimated distribution of runs with test
library(ggplot2);
ggplot(data = FREQS, aes(x = RR, y = Freq/k, fill = (Freq <= R_FREQ))) +
geom_bar(stat = 'identity') +
geom_vline(xintercept = match(R, FREQS$RR)) +
scale_fill_manual(values = c('Grey', 'Red')) +
theme(legend.position = 'none',
      plot.title      = element_text(hjust = 0.5, face = 'bold'),
      plot.subtitle   = element_text(hjust = 0.5),
      axis.title.y    = element_text(margin = margin(t = 0, r = 10, b = 0, l = 0))) +
labs(title    = 'Runs Test - Plot of Distribution of Runs under Exchangeability',
     subtitle = paste0('(Observed runs is black line, p-value = ', p, ')'),
     x = 'Runs', y = 'Estimated Probability'); 

---

$^\dagger$ I have broken the sequence up with dashes solely to make it easier to read; the dashes have no significance to the analysis.

Answer 4

Assuming the string of letters is long enough, you can apply Randomness tests on the data.

One set of such tests is called the diehard tests:

The diehard tests are a battery of statistical tests for measuring the quality of a random number generator. They were developed by George Marsaglia over several years and first published in 1995 on a CD-ROM of random numbers.

They involve a, perhaps arbitrary, set of tests such as:

• Birthday spacings
• Overlapping permutations
• Ranks of matrices
• Monkey tests
• Count the 1s
• Parking lot test
• Minimum distance test
• Random spheres test
• The squeeze test
• Overlapping sums test
• Runs test
• The craps test

A good sequence of random data should pass these tests.

However, passing these tests isn't sufficient to prove the numbers don't actually encode a real signal. They could be the output from a high-quality encryption routine.