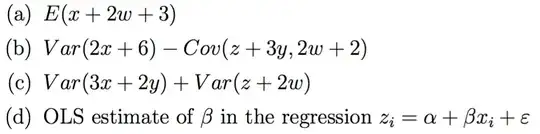Let's look at the situation. As a point of departure we will first study the bivariate standard Normal distribution. I will do this by plotting vertical slices through its graph: these are given by the functions
$$y\to \phi(x,y)$$
for $x = 0, \pm 1/2, \pm 1, \pm 3/2, \pm 2$ (where $\phi$ is the bivariate density). The reason for doing this is that variables $(X,Y)$ are independent if and only if the conditional distribution $Y\mid X=x$ does not vary with $x.$

As $x$ increases, the density grows smaller and the slices shrink down to the axis in the plots at the left. However, if we normalize these curves (rescaling each one vertically) so that each has unit area, thereby turning them into the conditional densities, they all coincide, as shown at the right. This is how we can tell $Y$ is independent of $X.$
Here is the same situation for a multivariate t distribution with $\nu=1$ degree of freedom (in two variables).
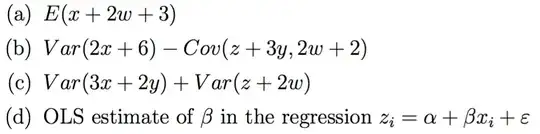
The conditional densities, although centered at $0,$ have different shapes: they vary with $x.$ You can see that they spread out as $|x|$ grows larger. This can (easily) be demonstrated algebraically by examining the formula for the multivariate t density.
Here is a "hand-waving" demonstration that might help us calibrate our intuition.
As Glen_b pointed out in comments, the Multivariate t is the distribution of standard multivariate Normal vector $X=(X_1,X_2,\ldots,X_d)$ divided by an independent positive variable $Z.$ (A multiple of $Z^2$ has a Gamma distribution, but that detail doesn't matter.)
Consider what happens to the preceding conditional distributions as $|X_1/Z|$ increases. When $|X_1/Z|$ is relatively large, it likely got that way through a combination of a large value of $|X_1|$ and a smaller than average value of $Z.$ Because $Z$ was small, and $Z$ simultaneously divides all the components of $X$, the values of $X_2/Z, X_3/Z, \ldots, X_d/Z$ (which obviously are scaled by the relatively large quantity $1/Z$) will thereby be more spread out. The larger $|X_1|$ gets, the larger $Z$ is likely to be and the more the other components are spread.
Because the conditional distributions of the $X_i/Z$ become more spread out as $|X_1/Z|$ increases, the $X_i/Z$ cannot be independent of $X_1/Z.$