Is the following statement true: Gradient descent is guaranteed to always decrease a loss function.
I know that if the loss function is convex, then each iteration of gradient descent will result in a smaller loss, but does this statement hold for all loss functions? Could we design a loss function in such a way that performing gradient descent was not optimal?
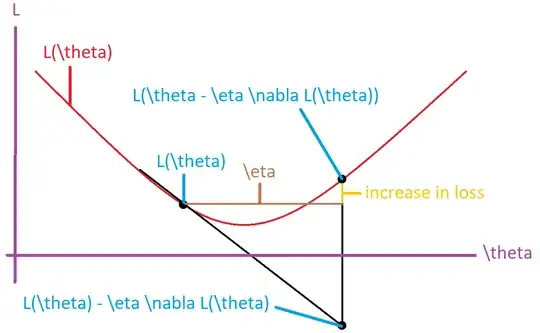
Whether the loss decreases depends on your step size. The direction opposite the gradient is that in which you should move to most quickly decrease your loss. A step of gradient descent is given by:
$$\theta_t = \theta_{t-1} -\eta\nabla_\theta\mathcal{L}$$
where $t$ indexes the training iteration, $\theta$ is the parameter, $\eta$ is the step size, and $\mathcal{L}$ is the loss. When you perform gradient descent, you are essentially linearizing your loss function around $\theta$. If $\eta$ is too large, then $\mathcal{L}(\theta_{t-1} -\eta\nabla_\theta\mathcal{L})$ may be greater than $\mathcal{L}(\theta_{t-1}) -\eta\nabla_\theta\mathcal{L}$, indicating that you overshot the local minimum and increased the loss (see illustration below). Note that it is also possible to overshoot the minimum and still have a decrease in loss (not shown).
