4

Let $X$ be an exponential random variable. I have been asked to evaluate whether each of the following is true or false and am seeking some insight about a solution that was offered.

$(a) E(X^2 |X>1) = E[(X+1)^2]\\(b) E(X^2 |X>1) = E(X^2) +1\\(c) E(X^2 |X>1) = (1 + E[X])^2$

The solution makes use of the following steps: $$ X - S | X >S = X \\ X | X>S = X + S\\X^2 | X > S = (X+S)^2 $$ Letting $S = 1$ we get that (a) is the correct answer, and (b) and (c) are not.

My issue with this is that the steps outlined do not seem intuitive and do not explain why the other two options are incorrect or inconsistent. Any explanation of this intuition or the concepts surrounding each step will be greatly appreciated.

whuber
  • 281,159
  • 54
  • 637
  • 1,101
Potato
  • 65
  • 5
  • Hi Potato, welcome to CV! Is this a question from a course or textbook? If so, please add the `[self-study]` tag & read its [wiki](https://stats.stackexchange.com/tags/self-study/info). – Jan Kukacka Oct 01 '18 at 09:59
  • 2
    Be careful concerning the subtle change in meaning of the "$=$" sign after "makes the following steps." It no longer means equality, but now has to be interpreted in the sense of "has the same distribution as." As far as your immediate question goes, you should have little trouble showing directly that the three right hand sides of (a), (b), (c) are all different, whence at most one of them can be correct. – whuber Oct 01 '18 at 13:53

1 Answers1

8

Intuition of Memorylessness

Let's visualize the memoryless property of exponential distributions.

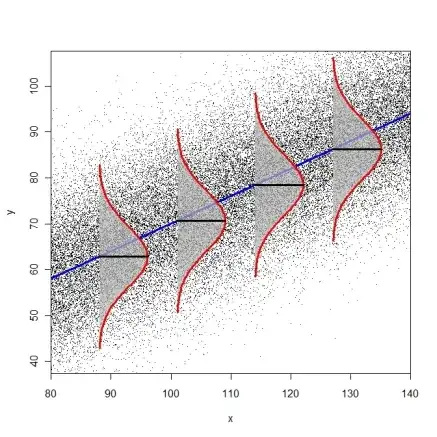
Figure 1: Exponential PDF and its truncation

The probability density function (PDF) represents the probability distribution by means of area. The horizontal axis represents values of a random variable $X.$ (The points where the graph has nonzero height extend from zero to infinity, but only values out to $2.5$ are shown.) The vertical axis represents probability density. The red shading denotes the area beneath all parts of the PDF where $X \gt 1.$ Restricting $X$ to a subset of its possible values, as in the subset determined by $X\gt 1,$ is called truncation.

Figure 2: Rescaling the truncated PDF

The axiom of total probability insists the area under an entire PDF is $1$ (100% probability). Truncation (obviously) decreases that area. We turn the truncated plot into a genuine PDF by scaling it--uniformly increasing its height--to make its area equal to $1.$ The vertical arrows depict that rescaling as a dynamic geometric operation, a uniform vertical stretching. (This implies the lengths of the arrows are proportional to the heights of the PDF where each originates.) The area beneath the original PDF is now shaded in blue to help you compare the two areas. The new red curve plots the conditional density of $X,$ written $X\mid X\gt 1$ in the question.

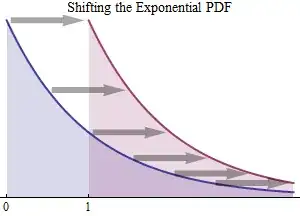
Figure 3: Shifting the PDF

The exponential PDF has a special property: when you shift the original PDF horizontally by $1,$ as shown by the horizontal arrows, it coincides with the rescaled truncated PDF. That this shift is constant is reflected in the constant lengths of all the arrows. (If they don't look all the same length, it's an optical illusion!)

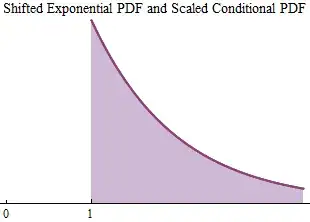
Figure 4

The purple shading in this final picture arises from the perfect coincidence of the blue (shifted) and red (rescaled truncated) areas. This relationship, "memorylessness," holds between the conditional distribution of $X\mid X \gt t$ and the original distribution shifted by $t$ for any positive number $t,$ equal to $X+t.$ Only exponential distributions are memoryless.

Application

Apply this intuition to the problem by replacing $X\mid X\gt 1$ (the red area in the last figure) by $X+1$ (the perfectly overlapping blue area in the last figure). The conclusion is that

$$E(X^2\mid X\gt 1) = E((X+1)^2).$$

Remaining questions

The other two answers cannot be correct because

$$E((X+1)^2) = E(X^2 + 2X + 1) = E(X^2) + 1 + 2E(X)$$

differs from $(b)$ by $2E(X)\ne 0$ and it differs from $(c)$ (whose value expands to $E(X)^2 + 1 + 2E(X)$) by $E(X^2) - E(X)^2 = \operatorname{Var}(X) \ne 0.$

Community
  • 1
whuber
  • 281,159
  • 54
  • 637
  • 1,101