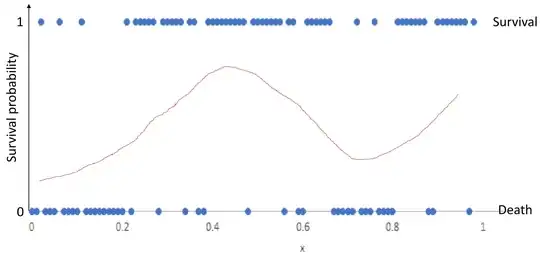
With this synthetic data set (the relationship between survival/death and the factor x) (plotted in the below figure as blue points), I would like to know how the survival probability depends on the factor x. I don't think logistic regression is the right tool for this data set because I think it can only give a monotonic function as its estimation while for this synthetic data set, I expect a different relationship (the red line in the below figure is my expectation). I wonder what is the best statistical tool here? generalized additive model?
Asked
Active
Viewed 345 times
4
-
3If you have information about time to death and not just the binary dead/alive classification, consider using survival analysis instead. Like a logistic regression, a Cox proportional hazards regression can also incorporate splines of continuous predictor variables as noted in the answer by @gung, for example via the `rms` package in R. – EdM Sep 27 '18 at 20:51
1 Answers
6
Logistic regression can very well model 'curvilinear' relationships, just as linear regression can. You need to add extra terms, functions of x to allow the model to account for that. The most common way is to add a sequence of polynomial terms (i.e., $x^2$, $x^3$, $x^4$, etc.). You can also use other nonlinear transformations of $x$ (e.g., $\log(x)$). A more sophisticated approach is to use spline functions.
There is an example of using logistic regression this way in my answer here: How to use boxplots to find the point where values are more likely to come from different conditions?
gung - Reinstate Monica
- 132,789
- 81
- 357
- 650
-
Thanks for your reply. In this sense, is additive model a more convenient tool? I'm not familiar with it but I guess additive model can provide a more convenient way to add nonlinearity to the model? – Tanis Sep 27 '18 at 19:57
-
@Tanis, what do you mean by "additive model" here? A simple model w/ x, x2, & x3, could well be called an additive model. – gung - Reinstate Monica Sep 27 '18 at 19:59
-
1I have this link to its wikipedia page. https://en.wikipedia.org/wiki/Generalized_additive_model – Tanis Sep 27 '18 at 20:01
-
@Tanis, OK, a GAM isn't quite the same as the generic use of "additive model". At any rate, you can think of a logistic regression with polynomial terms as a simple case of a GAM. Whether it's "more convenient" would only be a function of your relative comfort w/ the code. – gung - Reinstate Monica Sep 27 '18 at 20:10
-
There is one advantage of using regression splines in place og gam's (as in R's package `mgcv`): logistic regression with splines is a standard generalized linear model, so standard inference tools can be used. gam's on the other hand need special inference theory (and special software). – kjetil b halvorsen Sep 28 '18 at 09:14