Consider the normal product distribution, which is the distribution of the product of two or more independent normal variables. Particulary, focus in the case where the multiplied normal variables are $\mathcal{N}(0, 1)$.
Considering the following definition of subgaussian tail (taken from [1]):
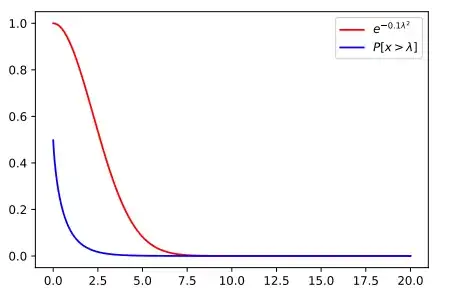
Does the normal product distribution have subgaussian tail?
I have been doing some numerical experiments which suggest an affirmative answer ($a=0.1$):
[1] Matoušek, J. (2008). On variants of the Johnson–Lindenstrauss lemma. Random Structures & Algorithms, 33(2), 142-156.