2

I have 118 microbes that I have tested at various concentrations of a drug that is supposed to kill them (0.1875 - 15). However, these microbes have mutations (A-H) which confer resistance to the drug and thus allow them to survive.

I would like to group these mutations into two clusters:

  • Mutations that confer high resistance
  • Mutations that confer low resistance

After doing some reading, I think that Expectation-Maximization is the right clustering methodology but I have two problems:

  1. The data are counts (e.g., how many bugs survived at that concentration)
  2. I need to group by the mutation

A simplified look at my data (e.g., for one drug) looks like the following (where A-H are the mutations): 

A <- c(0,0,0,0,0,0,0,4,1)
B <- c(0,0,0,9,7,3,1,0,0)
C <- c(0,0,0,3,8,0,1,0,0)
D <- c(0,0,0,0,0,10,5,4,1)
E <- c(0,0,0,0,1,3,2,1,0)
F <- c(0,0,0,6,8,0,3,3,0)
G <- c(0,0,0,0,0,13,5,3,0)
H <- c(0,0,0,0,0,7,4,2,0)

mydata        <- rbind(A,B,C,D,E,F,G,H)
mynames       <- c("0.1875","0.375","0.75","1.5","2.5","3.5","4.5","10","15")
mylegend      <- c("A","B","C","D","E","F","G","H")
mydata.labels <- c("0.1875","0.375","0.75","1.5","2.5","3.5","4.5","10","15")

So when you look at all 118 of them it looks like this: 

barplot(A+B+C+D+E+F+G+H, names=mynames, ylim=c(0,35))

All microbes

But when you separate them by mutations it looks like this. Looking carefully you can see that the distribution of some mutations is shifted to the right (e.g., A) and some to the left (maybe B or F):

barplot(as.matrix(mydata), ylim=c(0,15), beside=TRUE, col=rainbow(8), 
        names=mynames, legend=mylegend)

Microbes by mutation

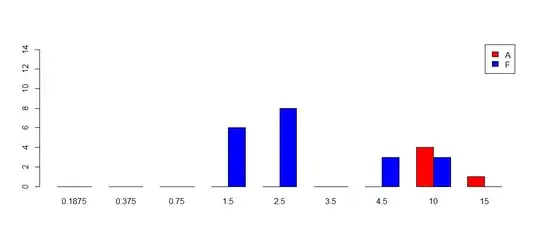
It is rather striking to look at two (A and F) which is why I want to split my mutations into a high/low grouping.

barplot(as.matrix(rbind(A,F)), ylim=c(0,15), col=c("red","blue"), beside=TRUE, 
        names=mynames, legend=c("A","F"))

enter image description here

I think that this is what E-M is for but I am not certain. It is not clear because I want to keep my groupings and I am working with counts.

Does anyone have any ideas on how to cluster my data into two groups that is not by eyeball? I tried just playing around with maximizing the group mean difference but it was not satisfying as it seemed somewhat arbitrary.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
Don Catanzaro
  • 21
  • 1
  • 1
    Expectation-Maximisation is actually for parameter learning (used for probabilistic models), not a clustering algorithm. Can you be a bit more specific on the problem you're trying to solve? You already have the clusters (i.e., high/low, mutation groups), you don't need to apply another clustering algorithm on it. Or did you mean you want to use an algorithm to find the groups rather than manually assigning them into groups? In which case have a look at K-means http://scikit-learn.org/stable/modules/clustering.html – swmfg Sep 26 '18 at 05:20
  • I don't know if I agree with the statement that EM is not a clustering algorithm. It is designed to find the hidden (latent) variables and yes it an be used for parameter learning but it is most definately a clustering technique. Ultimately I do want to assign the mutations to two groups (high/low) in a statistical manner, rather than by eye. It is my understanding that k-means is similar (if not a subset of EM - see https://stats.stackexchange.com/questions/76866/clustering-with-k-means-and-em-how-are-they-related) – user918967 Sep 26 '18 at 16:06
  • Do you know how many bugs were exposed for each combination of concentration & mutation? – gung - Reinstate Monica Sep 26 '18 at 17:48
  • All 118 bugs were exposed to each concentration and there are only 8 different types of mutations (A-H) – user918967 Oct 01 '18 at 15:08

0 Answers0