Elbow Test using AIC/BIC for identifying number of clusters using GMM

Question

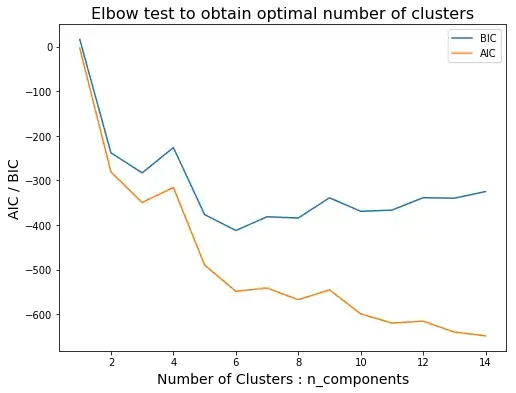
How to select number of clusters using GMM when the elbow test (AIC/BIC vs n_components) results in a graph like this?

Answer 1

Welcome to CV!

This plot shows how the AIC and BIC change as a function of the number of clusters. While the AIC continuous to decrease with a larger number of clusters, you can see that the BIC stops decreasing after $k=6$ clusters. For this reason, you could choose $k = 6$.

Another way to choose the 'best' number of clusters is by considering the elbow(s) of the figure. The elbow of a function is a point after which the decrease becomes notably smaller. An elbow is a heuristic, so there is no exact way to determine which value best describes this point. For example, one could argue that the AIC & BIC both stop decreasing as much after $k = 5$ clusters, while someone else might argue that this is after $k = 6$ clusters. You could even argue that the biggest decrease has already happened after $k = 2$ clusters.

Lastly, you don't have to choose any number of clusters just because AIC/BIC/whatever suggested you do so. If you have some a priori reason to assume that there should be $k = 3$ clusters, then that might be a better choice.

In short: An elbow in this context is a heuristic guide to decide the number of clusters if you have no other reason to assume a certain number of clusters.